Is it possible to get rid of exotic matter in warp drive?

On 1994, Miguel Alcubierre proposed a solution of the Einstein equations (see here) describing a space-time bubble moving at arbitrary speed. It is important to notice that no violation of the light speed limit happens because is the space-time moving and inside the bubble everything goes as expected. This kind of solutions of the Einstein equations have a fundamental drawback: they violate Weak Energy Condition (WEC) and, in order to exist, some exotic matter with negative energy density must exist. Useless to say, nobody has ever seen such kind of matter. There seems to exist some clue in the way Casimir effect works but this just relies on the way one interprets quantum fields rather than an evidence of existence. Besides, since the initial proposal, a great number of studies have been published showing how pathological the Alcubierre’s solution can be, also recurring to quantum field theory (e.g. Hawking radiation). So, we have to turn to dream of a possible interstellar travel hoping that some smart guy will one day come out with a better solution.

Of course, Alcubierre’s solution is rather interesting from a physical point of view as it belongs to a number of older solutions, like wormholes, time machines and like that, yielded by very famous authors as Kip Thorne, that arise when one impose a solution and then check the conditions of its existence. This turns out to be a determination of the energy-momentum tensor and, unavoidably, is negative. Then, they violate whatever energy condition of the Einstein equations granting pathological behaviour. On the other side, they appear the most palatable for science fiction of possible futures of space and time travels. In these times where this kind of technologies are largely employed by the film industry, moving the fantasy of millions, we would hope that such futures should also be possible.

It is interesting to note the procedure to obtain these particular solutions. One engineers it on a desk and then substitute them into the Einstein equations to see when are really a solution. One fixes in this way the energy requirements. On the other side, it is difficult to come out from the blue with a solution of the Einstein equations that provides such a particular behaviour, moving the other way around. It is also possible that such solutions are not possible and imply always a violation of the energy conditions. Some theorems have been proved in the course of time that seem to prohibit them (e.g. see here). Of course, I am convinced that the energy conditions must be respected if we want to have the physics that describes our universe. They cannot be evaded.

So, turning at the question of the title, could we think of a possible warp drive solution of the Einstein equations without exotic matter? The answer can be yes of course provided we are able to recover the York time, or warp factor, in the way Alcubierre obtained it with its pathological solution. At first, this seems an impossible mission. But the space-time bubble we are considering is a very small perturbation and perturbation theory can come to rescue. Particularly, when this perturbation can be locally very strong. On 2005, I proposed such a solution (see here) together with a technique to solve the Einstein equations when the metric is strongly perturbed. My intent at that time was to give a proof of the BKL conjecture. A smart referee suggested to me to give an example of application of the method. The metric I have obtained in this way, perturbing a Schwarzaschild metric, yields a solution that has an identical York time (warp factor) as for the Alcubierre’s metric. Of course, I am respecting energy conditions as I am directly solving the Einstein equations that do.

The identity between the York times can be obtained provided the form factor proposed by Alcubierre is taken to be 1 but this is just the simplest case. Here is an animation of my warp factor.

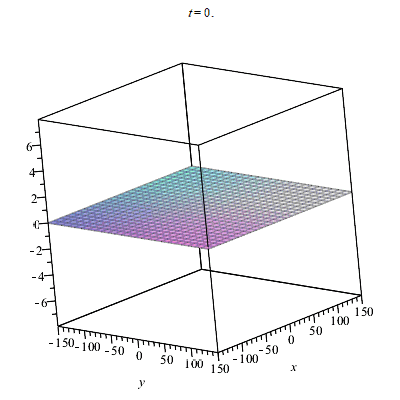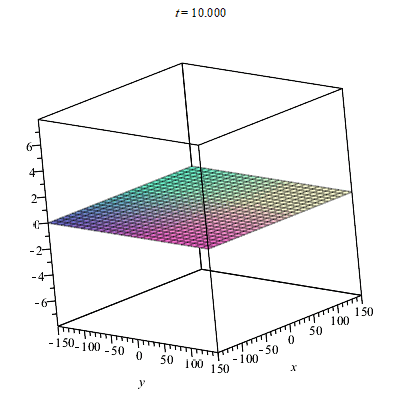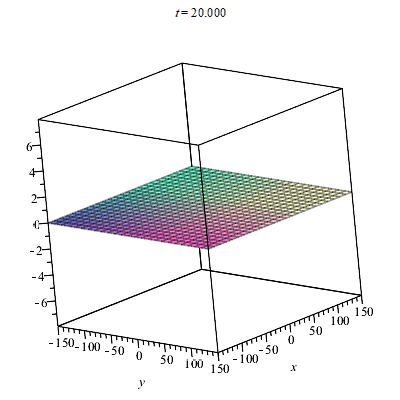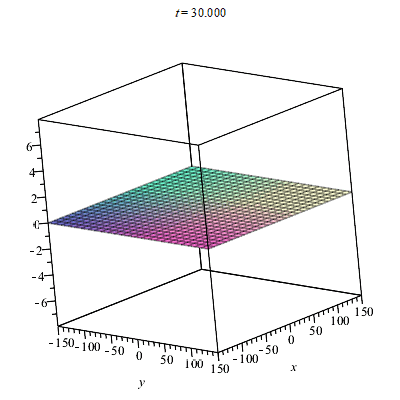
It seen the bubble moving as expected along the x direction.

My personal hope is that this will go beyond a mathematical curiosity. On the other side, it should be understood how to provide such kind of perturbations to a given metric. I can think to the Einstein-Maxwell equations solved using perturbation theory. There is a lot of literature about and a lot of great contributions on this argument.

Finally, this could give a meaning to the following video by NASA.