Spectrum of two color QCD

In a preceding post (see here) I have shown how SU(2) QCD can be reduced to a theory easily amenable to perturbation treatment. This case is quite easy as, due to the gauge group, algebra is not too much involved. At the leading order one gets the following set of equations

that are very easy to solve and so, we can get an understanding of the mass spectrum both for and the quark field. At a first glance we easily recognize that, at this order, is clear that QCD has a chiral symmetry and this symmetry arises naturally from the strength of the coupling .

At this stage we want just to write down the mass spectra. For the gluon field we have

exactly as for SU(3). The only change here should be the value of the string tension .Indeed, the folowing relation should hold and so, if one will have . This is in perfect agreement with lattice evidence (see here). This lattice evidence is quite old and should be pursued further. For a quark we have the spectrum

and as for the glueball spectrum we have and an elliptic integral. From this we say that the lowest state in the spectrum will have zero mass, the pion, and this is just a manifestation of the above approximate chiral symmetry.

The next step will be to go to higher orders and correct these results. But we see that, already at leading order, we conclude that the glueball spectrum must manifest itself at an experimental level exactly as happens to hadronic spectrum. Any other correction to it is just higher order.

QCD with two colors

Having an understanding of Yang-Mills theory grants the possibility to make QCD truly manageable and amenable to a perturbation treatment also in the infrared limit. A very easy example of this can be obtained working out the equations of QCD with two colors. In this case the gauge group is SU(2) and algebra is not too much involved. The relevant simplification is obtained via the “mapping theorem” (see my paper here). This theorem grants the existence of a leading order solution of Yang-Mills theory to do perturbation computations in the infrared limit by mapping it on a quartic massless scalar field through the so-called Smilga’s choice (see here). In turn this implies that in all QCD computations we have to manage just a scalar field making things simpler. In QCD with two colors we are reduced to the following action

being with Pauli matrices and Dirac matrices. So, classical equations of motion are

and we can do a strong coupling expansion by rescaling time as leaving us with the non-trivial leading order equations

and this set of equations is easily solved. We observe that at the leading order quarks can be considered massless (chiral simmetry) and the spectrum of the Yang-Mills theory is part of observational QCD. Finally, a discrete spectrum for quarks is also obtained whose ground state is zero, an expression of chiral symmetry. So, at this order, we expect pion mass to be zero and glueballs having no decay.

These are quite interesting results but higher order corrections should be exploited to have a clear understanding of all physics. Essentially, we would like to compute the pion mass, i.e. to see the breaking of the chiral symmetry seen at the leading order, and the decay width of the lowest glueball state. I will exploit computations to higher orders to reach such aims.

Smilga’s choice and the mapping theorem

After the acceptance of my paper (see here) I wondered what should have been Smilga’s choice for the SU(3) given its existence. Let me explain what a Smilga’s choice is. Firstly I point out his beatiful book about QCD that was my starting point for all this matter (see here). You will find in this book, in the chapter about classical solutions, that when one chooses a set of values different from zero of the components of the Yang-Mills potential and take these non-null components all equal one gets for space-homogeneous Yang-Mills equations the motion equation of a massless anharmonic oscillator. Smilga asked in the book what the physical meaning of such homogeneous solutions should be. I answered to this smart question with a mapping theorem (take a look at my paper here): Anytime a Smilga’s choice is done one has mapped a solution of the classical Yang-Mills equations onto a solution of a quartic massless scalar field. This result is extremely important as we obtain in this way both the physical meaning of such solutions and a set of classical solutions to do perturbation theory without recurring to some small parameter. Indeed, we know how to manage a quantum scalar field in the strong coupling limit (see here and here).

Now, for SU(2) it is very easy to do a choice that reaches our aim: One takes

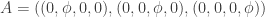
and you are done. I have not exploited all the phase space in this case as one should consider that Smilga’s choice is not unique and things get worse as the gauge group is taken more complex. For SU(3) things are really horrible as one has to explore a very large phase space and the product of the structure constants of the group does not admit a simple expression. So, I reduced myself to write down a few lines of code both in C and matlab working out such a product of structure constants. My PC worked fine for me and obtained a lot of results. As said above Smilga’s choice is not unique and one can have a huge number of choices increasing the number of structure constants of the group. So, e.g. the following Smilga’s choice is good for SU(3) leaving you with the right ‘t Hooft coupling in the mapped scalar field

This Smilga’s choice gives a multiplicative overall factor 2 to the scalar field action. Smilga’s choice for SU(2) will leave a factor -3. Of course, these factors will depend on the gauge group but one can ask a couple of mathematical questions that are worth exploring. Firstly, whatever Smilga’s choice one takes that grants the correct ‘t Hooft coupling in the Lagrangian of the scalar field, is the overall factor always the same? Better, does a Smilga’s choice exist that grants for any SU(N) group the same overall factor equal in absolute value to the number 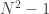as happens to SU(2)?  These results would extend the understanding of the existence of the mapping to a stunning level taking into account that already for SU(3) the number of configurations is really overwhelming.

Concluding, we just remark the essential points to be taken into account for a choice to be a proper Smilga’s choice: 1) The proper Lagrangian of a quartic massless scalar field should be reproduced multiplicated with an overall factor (negative or positive is not important). 2) The coupling of the scalar field must be the ‘t Hooft coupling for a Yang-Mills theory with a SU(N) gauge group and coupling constant .

Update: Found! After I have extended the search space with my C program, I was able to obtain a set of proper Smilga’s choices for SU(3). These behave exactly as for SU(2). Here is an example

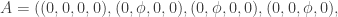
This gives an overall factor and the proper ‘t Hooft coupling with the same signs in the Lagrangian of the scalar field as seen for the SU(2) case, that is one has in the end the following mapped Lagrangian

and things are done! We are left we an interesting mathematical question: As the gauge group is changed the number of proper Smilga’s choices increases vastly. What should be the meaning of such a large number? What kind of symmetry is hidden behind this?

An inspiring paper

These days I am closed at home due to the effects of flu. When such bad symptoms started to relax I was able to think about physics again.  So, reading the daily from arxiv today I have uncovered a truly inspiring paper from Antal Jakovac a and Daniel Nogradi (see here). This paper treats a very interesting problem about quark-gluon plasma. This state was observed at RHIC at Brookhaven. Successful hydrodynamical models permit to obtain values of physical quantities, like shear viscosity, that could be in principle computed from QCD. The importance of shear viscosity relies on the existence of an important prediction from AdS/CFT symmetry claiming that the ratio between this quantity and entropy density can be at least . If this lower bound would be proved true we will get an important experimental verification for AdS/CFT conjecture.

Jakovac and Nogradi exploit the computation of this ratio for SU(N) Yang-Mills theory. Their approach is quite successful as their able to show that the value they obtain is still consistent with the lower bound as they have serious difficulties to evaluate the error. But what really matters here is the procedure these authors adopt to reach their aim making this a quite simple alley to pursuit when the solution of Yang-Mills theory in infrared is acquired. The central point is again the gluon propagator. These authors assume simply the very existence of a mass gap taking for the propagator something like in Euclidean time. Of course, is the glueball mass. This is a too simplified assumption as we know that the gluon propagator is somewhat more complicated and a full spectrum of glueballs does exist that can contribute to this computation (see my post and my paper).

So, I spent my day to extend the computations of these authors to a more realistic gluon propagator.  Indeed, with my gluon propagator there is no need of one-loop computations as the identity at 0-loop does not hold true anymore for a non-trivial spectrum and one has immediately an expression for the shear viscosity. I hope to give some more results in the near future.

LHC will stop for at least eight months

The damages following LHC accident, occurred last month, are more serious than expected. Some design errors have been identified into the valves that should regulate the quantity of helium flowing in such cases. Helium entered inside the ring and the valves were underdimensioned for the aims. Bad news is that repairing damages will require at least eight months. Optimistically one can hope starting of operation on May or June 2009. An article can be read in Nature about (see here). Dynamics of the accident is given by CERN here.

Physics Letters B at last!

Yesterday, the Editor of Physics Letters B communicated to me that my paper (see here) was accepted for publication. This was great for at least one reason: Physics Letters B is one of the most important journals in our area of activity and the paper that was accepted gives a sensible mathematical proof of the form of the gluon and ghost propagators in the infrared and relative mass spectrum that implies the very existence of a mass gap for the Yang-Mills theory. The key theorem is what I called the “mapping theorem” where a SU(N) Yang-Mills theory is mapped on a theory whose solution in the low energy limit I presented here and Physical Review D (see here). This analysis is in perfect agreement with the scenario emerging from lattice computations but we have the nice situation of explicit formulas for the gluon propagator and the spectrum permitting explicit computations wherever needed.

Also in this case the peer-review system worked at best. Both Editor and referees permitted to correct what appeared a serious difficulty in the proof of the mapping theorem. Once I solved this the paper was straightforwardly approved for publication. I take this chance to thank them all publicly.

I give here the formulas for the gluon propagator in the Landau gauge (the ghost propagator is that of a free particle) and the spectrum:

being

and

being an integration constant of Yang-Mills theory, arising from conformal invariance, to be fixed experimentally and an elliptic integral that is about 1.3111028777. From the mass spectrum is clearly seen the mass gap when is taken. Nature decides what is but an higher order theory should be able to derive it. We see that the spectrum of the theory is made of massive excitations that should not be called gluons. I think that glueballs is more appropriate.

So, this is a key moment for Yang-Mills theory. It implies a great understanding of the behavior of the theory in a regime not accessible before. Knowing the gluon propagator means that a Nambu-Jona-Lasinio model describes correctly the phenomenology at low energies. This we proved quite recently (see this post).

A new point of view

Today in arxiv appeared a work by Christian Fischer, Axel Maas and Jan Pawlowski (see here). This work is relevant because, for the first time, three authors that defended functional method so strongly now acknowledge the very existence of another solution in the infrared for the Dyson-Schwinger equations for Yang-Mills theory. Indeed they properly cite the work of Boucaud et al. (see recent preprint) and Aguilar, Binosi and Papavassiliou (see here) that found such solution with Dyson-Schwinger equations. I would like to say that these authors find a scenario that agreed with mine and lattice computations (see here and my contribution here). This approach has the fault that does not give a closed form to the gluon propagator permitting computations or, at least, to prove the existence of a mass gap. This means that the utility of such understanding, while very important, has some limitations.

Fischer, Maas and Pawlowski paper contains an important new result that none considered before. They prove that the solution that agreed with the scenario seen on the lattice violates BRST invariance. The reason why this is a striking result is that this is what one expects if the particles in the theory acquire a mass. They correctly observe that the gluon acquires a kind of screening mass and cannot be considered a true massive particle. This is truly beautiful because we know that the true carriers of the strong force in the infrared are bounded states of gluons that should be better named glueballs. They also show, but this was an expected result, that the gluon propagator in the infrared has the same behavior independently on the number of colors.

I would like to conclude with praise to this beatiful work that I hope it will appear soon in the published literature. The change of point of view of these researchers has been of great moment.

Localization with off-diagonal disorder

Today, the Editor of International Journal of Modern Physics B communicated to me that my paper (see here) has been accepted for publication. This paper presents an application of my strong perturbation method to a typical condensed matter system having off-diagonal disorder. The interesting thing about is that this system is not localized for the state with zero energy. The perturbation series I get has the development parameter given by the ratio between coherence time and Fermi time, exactly the opposite of a weak localization scheme.

This paper has an interesting story. Writing down it I did not emphasize the essential fact that I was discussing a system with off-diagonal disorder. Finally, the referee hit the point and the paper has been accepted with a proper revision. This is again a lesson, if needed, that when the peer-review method works fine it is an advantage for all the community and there is a lot to gain both for authors and journals.

Nicola Cabibbo and the Nobel prize

Nicola Cabibbo has been a teacher of mine at University “La Sapienza” in Rome. He taught me quantum field theory and I firstly got exposed to this beautiful construction of human mind through his wonderful lessons. I still have a vivid recollection of these lectures in the same room where Marcello Conversi explained us a lot of phenomenology ranging from blackbody radiation to Fermi theory of beta decay. Cabibbo was also my thesis advisor and he was there when I discussed it at my final “laurea” examination. So, I have a lot of reasons to regret for a missing deserved prize to him. I have read this article on Physics World and so memories flowed down. I have met him recently at Accademia dei Lincei in Rome. That was when Sergio Ferrara come there to talk about supersymmetry (see here). Cabibbo awarded Ferrara with a medal of the Accademia and it was a very nice moment.

I should say that Cabibbo’s lectures about QFT are still in my mind and I mantain memos of them on my shelves. Anyhow, Cabibbo is part of history of physics. No prize can change this or change the role he had in the development of particle physics.

Nambu, Kobayashi and Maskawa

It is appeared the announcement of the Royal Swedish Academy for the 2008 Nobel prize in physics (see here).  The prize has been awarded to Yoichiro Nambu, Makoto Kobayashi and Toshihide Maskawa. Yoichiro Nambu has been awarded for his discovery of spontaneous breaking of simmetry in particle physics. A pair of fundamental papers about this fundational issue were written in collaboration with Giovanni Jona-Lasinio. These were the starting point of an idea that permeates the standard model. Kobayashi and Maskawa extended the idea due to Nicola Cabibbo of a quark mixing. Together with the Higgs mechanism this generated the idea that, in order to reproduce the observed pattern of CP violation, one should have at least three quark families. This prediction was confirmed with the observation of bottom and top quarks.