A first paper on square root of a Brownian motion and quantum mechanics gets published!

Following my series of posts on the link between the square root of a stochastic process and quantum mechanics (see here, here, here, here, here), that I proved to exist both theoretically and experimentally, I am pleased to let you know that the first paper of my collaboration with Alfonso Farina and Matteo Sedehi was finally accepted in Signal, Image and Video Processing. This paper contains the proof of what I named the “Farina-Frasca-Sedehi proposition” in my paper that claims that for a well localized free particle there exists a map between the wave function and the square root of binomial coefficients. This finally links the Pascal-Tartaglia triangle, given through binomial coefficients, to quantum mechanics and closes a question originally open by Farina and collaborators on the same journal (see here). My theorem about the square root of a stochastic process also appears in this article but without a proof.

Marco Frasca (2012). Quantum mechanics is the square root of a stochastic process arXiv arXiv: 1201.5091v2

Farina, A., Giompapa, S., Graziano, A., Liburdi, A., Ravanelli, M., & Zirilli, F. (2011). Tartaglia-Pascal’s triangle: a historical perspective with applications Signal, Image and Video Processing DOI: 10.1007/s11760-011-0228-6

Unbreakable

Today, at HCP2012, new results on Higgs boson search were made available by CMS and ATLAS. Of course, well aligned with preceding rumors, all in all these appear rather disappointing. Maybe, beyond the increasing agreement with Standard Model expectations, the most delusional result is that the particle announced on July 4th appears to be completely lonely on a desert ranging till almost 1 TeV, at least if one is looking for other Higgs particles behaving Standard Model-like. decay rate is now aligning with expectations even if there is some room for a different outcome. On the other side, both experiments did not update findings. The scenario that is emerging from these results is the theorist’s nightmare. Tomorrow, all this will be collected in single talks by CMS and ATLAS speakers.

In a retrospective we could say that people claiming for a prize to discoverers of the Higgs mechanism seem to be vindicated. There appears no sign of supersymmetry that is more and more relinquished in a nowhere land. But, I would like to point out that, if a supersymmetric theory is the right one, there is just one theory to be singled out exploring the parameter space. It is normal in any case to see such a vast epidemic death of theories. It is also possible that theorists should now do a significant effort for new proposals beyond those largely explored in these last thirty years.

Standard Model is even more resembling a perfect theory really unbreakable and mimicking the success of the Maxwell equations put forward 150 years ago.  But we know it must break…

Finally, I would like to conclude this rather fizzling out post by pointing out a rather funny side of this situation. Tommaso Dorigo has a bet on with Gordon Watts and Jacques Distler amounting to $1200 on the non-existence of SUSY partners. This bet has not been payed yet as Distler is claiming there are a lot of “juicy rumors” from CERN and the terms are not fulfilled yet (see comments here).  I do not know what rumors Distler is talking about but, unless CERN is not hiding data (that would appear a rather strange behavior at best), maybe it is time to do a check on who the winner could be.

Kyoto, arXiv and all that

Today, Kyoto conference HCP2012 has started. There is already an important news from LHCb that proves for the first time the existence of the decay . They find close agreement with the Standard Model (see here). Another point scored by this model and waiting for new physics yet. You can find the program with all the talks to download here. There is a lot of expectations from the update on the Higgs search: The great day is Thursday. Meantime, there is Jester providing some rumors (see here on twitter side) and seem really interesting.

I have a couple of papers to put to the attention of my readers from arXiv. Firstly, Yuan-Sen Ting and Bryan Gin-ge Chen provided a further improved redaction of the Coleman’s lectures (see here). This people is doing a really deserving work and these lectures are a fundamental reading for any serious scholar on quantum field theory.

Axel Weber posted a contribution to a conference (see here) summing up his main conclusions on the infrared behavior of the running coupling and the two-point functions for a Yang-Mills theory. He makes use of renormalization group and the inescapable conclusion is that if one must have a decoupling solution, as lattice computations demand, then the running coupling reaches an infrared trivial fixed point. This is in close agreement with my conclusions on this matter and it is very pleasant to see them emerge from another approach.

Sidney Coleman (2011). Notes from Sidney Coleman’s Physics 253a arXiv arXiv: 1110.5013v4

Axel Weber (2012). The infrared fixed point of Landau gauge Yang-Mills theory arXiv arXiv: 1211.1473v1

Breaking of a symmetry: A paper

I have uploaded a paper on arXiv (see here), following my preceding post,  where I show that supersymmetry has inside itself the seeds for the breaking. I consider a Wess-Zumino model without masses (chiral) and I prove that, at lower momenta, it boils down to a Nambu-Jona-Lasinio model so, breaking supersymmetry through a gap equation that has a solution beyond a critical coupling. An essential assumption is that the coupling in the model is not increasingly smaller but rather increasingly greater. So, bosons and fermions get different masses.

This should open up a new way to see at supersymmetric theories that produce by themselves nonlinearities: It is enough to have such nonlinearities growing bigger. In this way, the large number of parameters that seems a need in the Minimal Supersymmetric Standard Model, arising from the introduction by hand of breaking terms, hopefully should reduce significantly.

Finally, I would like to point out a paper by Jamil Hetzel giving a nice introduction to these problematics (see here). This is a master thesis whose content appeared on JHEP.

Marco Frasca (2012). Chiral Wess-Zumino model and breaking of supersymmetry arXiv arXiv: 1211.1039v1

Jamil Hetzel (2012). Probing the supersymmetry breaking mechanism using renormalisation group
invariants arXiv arXiv: 1211.1157v1

Breaking of a symmetry

This week-end has been somewhat longer in Italy due to November 1st holiday and I have had the opportunity to read a very fine book by Ian Aitchison: Supersymmetry in Particle Physics – An Elementary Introduction. This book gives a very clear introduction to SUSY with all the computations clearly stated and going into the details of the Minimal Supersymmetric Standard Model (MSSM). This model was originally proposed by Howard Georgi and Savas Dimopolous (see here) and today does not seem to be in good shape due to recent results from LHC. Authors introduce a concept of a “softly” broken supersymmetry to accomodate the Higgs mechanism in the low-energy phenomenology.  A “soflty” broken supersymmetry is when the symmetry is explicitly broken using mass terms but keeping renormalizability and invariance under the electroweak symmetry group. The idea is that, in this way, the low-energy phenomenology will display a standard Higgs mechanism with a vacuum expectation value different from zero. This fact is really interesting as we know that in a standard electroweak theory the symmetry cannot be explicitly broken as we lose immediately renormalizability but a supersymmetric theory leaves us more freedom. But why do we need to introduce explicit breaking terms into the Lagrangian of the MSSM? The reason is that SUSY is conveying a fundamental message:

There is no such a thing as a Higgs mechanism.

Indeed, one can introduce a massive contribution to a scalar field, the term, but this has just the wrong sign and, indeed, a spontaneously broken supersymmetry is somewhat of a pain. There are some proposed mechanisms, as F or D breaking fields or some dynamical symmetry breaking, but nothing viable for the MSSM. Given the “softly” breaking terms, then the argument runs smoothly and one recovers two doublets and 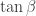parameter that some authors are fond of.

The question at the root of the matter is that a really working supersymmetry breaking mechanism is yet to be found and should be taken for granted as we do not observe superpartners at accessible energies and LHC has yet to find one if ever. This mechanism also drives the electroweak symmetry breaking. Indeed, supersymmetry properly recovers a quartic self-interaction term but the awkward quadratic term with a wrong sign gives serious difficulties. Of course, the presence of a quartic term into a scalar field interacting with a fermion field, e.g. a Wess-Zumino model, provides the essential element to have a breaking of supersymmetry at lower energies: This model is reducible to a Nambu-Jona-Lasinio model and the gap equation will provide a different mass to the fermion field much in the same way this happens to chiral symmetry in QCD. No explicit mass term is needed but just a chiral model.

This means that the MSSM can be vindicated once one gets rid of an explicit breaking of the supersymmetry and works out in a proper way the infrared limit. There is a fundamental lesson we can learn here: SUSY gives rise to self-interaction and this is all you need to get masses. Higgs mechanism is not a fundamental one.

Dimopoulos, S., & Georgi, H. (1981). Softly broken supersymmetry and SU(5) Nuclear Physics B, 193 (1), 150-162 DOI: 10.1016/0550-3213(81)90522-8

Marco Frasca (2011). Chiral symmetry in the low-energy limit of QCD at finite temperature Phys. Rev. C 84, 055208 (2011) arXiv: 1105.5274v4