
After CERN’s updates (well recounted here, here and here) producing no real news but just some concern about possible Higgs cloning, I would like to discuss here some mathematical facts about what one should expect about mass generation and why we should not be happy with these results, now coming out on a quarterly basis.
The scenario we are facing so far is one with a boson particle resembling more and more the Higgs particle appearing in the original formulation of the Standard Model. No trace is seen of anything else at higher energies, no evidence of supersymmetry. It appears like no new physics is hiding here rather for it we will have to wait eventually the upgrade of LHC that will start its runs on 2015.
I cannot agree with all of this and this is not the truth at all. The reason to not believe all this is strictly based on theoretical arguments and properties of partial differential equations. We are aware that physicists can be skeptical also about mathematics even if this is unacceptable as mathematics has no other way than being true or false. There is nothing like a half truth but there are a lot of theoretical physicists trusting on it. I have always thought that being skeptical on mathematics is just an excuse to avoid to enter into other work. There could always be the risk that one discovers it is correct and then has to support it.
The point is the scalar field. A strong limitation we have to face when working in quantum field theory is that only small coupling can be managed. No conclusive analysis can be drawn when a coupling is just finite and also lattice computations produce confusion. It seems like small coupling only can exist and all the theory we build are in the hope that nature is benign and yields nothing else than that. For the Higgs field is the same. All our analysis are based on this, the hierarchy problem comes out from this. Just take any of your textbook on which you built your knowledge of this matter and you will promptly realize that nothing else is there. Peschin and Schroeder, in their really excellent book, conclude that strong coupling cannot exist in quantum field theory and the foundation of this argument arises from renormalization group. Nature has only small couplings.
Mathematics, a product of nature, has not just small couplings and nobody can impede a mathematician to take these equations and try to analyze them with a coupling running to infinity. Of course, I did it and somebody else tried to understand this situation and the results make the situation rather embarrassing.
These reflections sprang from a paper appeared yesterday on arxiv (see here). In a de Sitter space there is a natural constant having the dimension of energy and this is the Hubble constant (in natural units). It is an emerging result that a massless scalar field with a quartic interaction in such a space develops a mass. This mass goes like  being
being  the coupling coming from the self-interaction and
the coupling coming from the self-interaction and  the Hubble constant. But the authors of this paper are forced to turn to the usual small coupling expansion just singling out the zero mode producing the mass. So, great news but back to the normal.
the Hubble constant. But the authors of this paper are forced to turn to the usual small coupling expansion just singling out the zero mode producing the mass. So, great news but back to the normal.
A self-interacting scalar field has the property to get mass by itself. Generally, such a self-interacting field has a potential in the form  and we can have three cases
and we can have three cases  ,
, 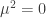 and
and  . In all of them the classical equations of motion have an exact massive free solution (see here and Tao’s Dispersive Wiki) when
. In all of them the classical equations of motion have an exact massive free solution (see here and Tao’s Dispersive Wiki) when  is finite. These solutions cannot be recovered by any small coupling expansion unless one is able to resum the infinite terms in the series. The cases with
is finite. These solutions cannot be recovered by any small coupling expansion unless one is able to resum the infinite terms in the series. The cases with 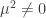 are interesting in that this term gets a correction depending on
are interesting in that this term gets a correction depending on  and for the case
and for the case  one can recover a spectrum with a Goldstone excitation and the exact solution is an oscillating one around a finite value different from zero (it never crosses the zero) as it should be for spontaneous breaking of symmetry. But the mass is going like
one can recover a spectrum with a Goldstone excitation and the exact solution is an oscillating one around a finite value different from zero (it never crosses the zero) as it should be for spontaneous breaking of symmetry. But the mass is going like 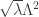 where now
where now 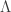 is just an integration constant. The same happens in the massless case as one recovers a mass going like
is just an integration constant. The same happens in the massless case as one recovers a mass going like  . We see the deep analogy with the scalar field in a de Sitter space and these authors are correct in their conclusions.
. We see the deep analogy with the scalar field in a de Sitter space and these authors are correct in their conclusions.
The point here is that the Higgs mechanism, as has been devised in the sixties, entails all the philosophy of "small coupling and nothing else" and so it incurs in all the possible difficulties, not last the hierarchy problem. A modern view about this matter implies that, also admitting  makes sense, we have to expand around a solution for
makes sense, we have to expand around a solution for  finite being this physically meaningful rather than try an expansion for a free field. We are not granted that the latter makes sense at all but is just an educated guess.
finite being this physically meaningful rather than try an expansion for a free field. We are not granted that the latter makes sense at all but is just an educated guess.
What does all this imply for LHC results? Indeed, if we limit all the analysis to the coupling of the Higgs field with the other fields in the Standard Model, this is not the best way to say we have observed a true Higgs particle as the one postulated in the sixties. It is just curious that no other excitation is seen beyond the (eventually cloned) 126 GeV boson seen so far but we have a big desert to very high energies. Because the very nature of the scalar field is to have massive solutions as soon as the self-interaction is taken to be finite, this also means that other excited states must be seen. This simply cannot be the Higgs particle, mathematics is saying no.
M. Beneke, & P. Moch (2012). On “dynamical mass” generation in Euclidean de Sitter space arXiv arXiv: 1212.3058v1
Marco Frasca (2009). Exact solutions of classical scalar field equations J.Nonlin.Math.Phys.18:291-297,2011 arXiv: 0907.4053v2



 Posted by mfrasca
Posted by mfrasca  Yesterday, at the
Yesterday, at the  I would like to spend a few words here to let my readers know what is at stake here. On 1975, NASA launched the
I would like to spend a few words here to let my readers know what is at stake here. On 1975, NASA launched the 
