Gluons are not all the story: An update

In a recent post of mine (see here) I have pointed out to you a beautiful paper by Dan Pirjol and Carlos Schat. This paper is now appeared on Physical Review Letters (see here) but you can find also the preprint on arxiv (see here). I think its content is really important as it gives a serious clue toward our understanding of low-energy QCD. Dan agreed to publish here a contribution about his work and I am glad to post it.

We find that, within experimental errors on the hadron masses, the
so-called gluon-exchange model (OGE) is disfavored by data. This is probably not very  surprising, since at low energies the real degrees of freedom of QCD should include, in addition to the  gluons, also pions (the Goldstone bosons of the spontaneously broken  chiral symmetry). The OGE model does not include the pion exchange effects; an alternative to the OGE model  which includes their effects is the so-called GBE (Goldstone boson exchange) model.

There has been a long-standing debate about the most appropriate model
of quark forces in the framework of the constituent quark model, in  particular about their spin-flavor dependence. The main candidates are
the OGE and GBE models (see e.g. the second paper in Ref.[3] for a
discussion of this controversy). Our letter attempts to resolve this controversy using only minimal assumptions about the orbital dependence
of the hadronic wave functions. More precisely, we assume only isospin
symmetry, but no other assumption is made about the form of the wave
functions. The novel mathematical tool which makes our analysis possible is the application of the permutation group , which allows one to study the implications of the most general spin-flavor structure of the quark forces.

Sigma resonance again

José Pelaéz and Guillermo Rìos published today a paper on arxiv (see here). The argument is an understanding of the nature of and resonances. The technique they use is Chiral Perturbation Theory (ChPT) but the idea is to see the behavior of the amplitudes at increasing number of colors. They get again a confirmation that the very nature of is not a typical state. Rather, a subdominant component is seen at larger energies with larger values of the number of colors. This conclusion  agrees with our theorem proved here.

The current situation forces the authors to prudence. They do not draw any conclusion about the real nature of and but their results still appear impressive. These authors have a long file of very good works about the quest for an understanding of the lower part of QCD spectrum and they have given the mass and the width of   with really increased precision. They belong to a group headed by Paco Yndurain. You can find a tribute to Paco by Stephan Narison here.

From my view you can see this as another confirmation to the idea that is a glueball and the lowest state of a pure Yang-Mills theory. This evidence is becoming overwhelming but other interpretations are not ruled out yet. The fact that or else f0(980) are glueballs would give further strong support to this as I expect a glueball state at this value of energy.

A review on proton spin

As you may know, there is a lot of experimental activity to understand as the spin of the proton can arise from its components, i.e. quarks and gluons. The great difficulties we have to manage low-energy QCD makes this problem fundamental toward an improved comprehension of this limit. In arxiv today an interesting review by Steven Bass is appeared (see here and here). Bass gives a brief  overview of the current situation mostly from the experimental side. As reader from this blog may know (see here), glue contribution to spin is about zero and the proton spin appears mostly due to valence quarks and their interplay with vacuum. Indeed this is Bass’ conclusion and we fully agree with it.

The emerging scenario is really striking. It appears that QCD behavior in a non-perturbative regime goes completely off known tracks. This implies that there is a lot of problems to be solved in the future for us working in this field.

NIF at start

National Ignition Facility started this year at Lawrence Livermore Laboratories. This project has the ambition to give an answer to our quest for nuclear fusion as a reliable source of energy.Funded by US government, it has implied delays and cost increase during its realization. But the aims are so relevant that this is worthwhile spent money. The approach for this experiment is that of inertial fusion. This technique uses power lasers to hit a pellet of fusion material. Pressure of light, when applied uniformly on the target, will push nuclei so near to win the effect of the Coulomb barrier and so they start to fuse each other relaxing a large amount of energy. This is our dream of a sun on earth. I think people is also aware of the other way research is pursuing through tokamak where a plasma is heated through different means to achieve the same goal. For this track, ITER is still at very start of its realization.

As usual,  there is a very good article on the New York Times about NIF (see here).  The hope is to solve one of the most difficult problems of humankind. So, we can only wish the best of lucks at NIF.

Pioneers

Jeffrey Mandula is a well-knwon theoretical physicist whose main result, Coleman-Mandula theorem, opened the road to the discovery of supersymmetry. But Mandula is also known for his pioneering works on lattice QCD. Looking back to old papers on the question of the Yang-Mills propagators, I have found two beautiful papers by Mandula and Ogilvie (see here and here) published in the eighties, where they arrive to the following conclusion

From the behavior of the gluon propagator reported here, it appears that in pure Yang-Mills theory, a dynamical Higgs phenomenon occurs. Our best estimate of the effective gluon mass, as determined at large distances, is about 600 MeV, with finite size effects, possible scaling violations, and statistical uncertainties of at least . In analogy with the concept of a constituent quark mass, it may be useful to think of the mass in the gluon propagator as a constituent gluon mass. The massiveness of the gluon may be connected to the apparent suppression of many-gluon intermediate states in decay, and the relative absence of the mixing between the lowest quark model states and those with gluonic excitations.

They used small lattices due to the computer limitations at that time and ideas about infrared behavior of Yang-Mills theory were just beginning to flourish. But, with our hindsight, we should emphasize the deep intuition that these authors put forward when such analysis were just starting. Besides, resonance was not yet seen and their estimate of the gluon mass appears really good.

As you may know, after these works, things took a different turn and for a long time since now we have been coping with a different scenario from that devised by Mandula and Ogilvie that took the scenes and not yet left them. This scenario appears today to be in a serious difficulty against lattice computations but people do not generally agree about what the right view should be, making painfully slow truth achievement .

Cramer-Rao bound and Ricci flow II

The paper I presented about this matter (see here) has been accepted by EuRad 2009 Conference. This will result in a publication in IEEE Proceedings. IEEE is the most important engineering society. I cannot made public this paper until it will appear in the proceedings. After this date you can read it at IEEE Xplore where you can find another paper of mine about scattering of electromagnetic waves by a rough surface (see here). As you can see, the way publishing is operated by engineers is quite different from that of physicists.

Anyhow, the idea is quite simple and use the fact that for a two-dimensional Riemann manifold one has always a conformal metric. Then, Fischer information matrix can be expressed in a diagonal form with new estimators that are always optimal with respect to Cramer-Rao bound. So, due to the fact that there exists a vast set of probability distributions with two parameters, the application areas of this result are huge. In my paper I make the case of sea clutter for radar applications but what I prove is a theorem in statistics and you can realize by yourself the importance.

The n-parameter case can also be made but here there are two more demanding requests: the existence of a conformal metric and the existence of a potential for a vector field that satisfies Liouville equation. These cannot always be satisfied and so the two-dimensional case appears a rather lucky one.

A beautiful paper on arxiv

Keeping on their way of producing sound work, Bogolubsky, Ilgenfritz, Mueller-Preussker and Sternbeck have got their paper (see here) published on Physics Letters B. This is a collaboration between people working in Russia, Germany and Australia. The main aim of this work is the computation on a lattice of the two-point functions and the running coupling of a pure Yang-Mills theory. They carry on lattice computations from to points entering into a deep enough infrared limit to get a meaningful behavior of the lattice theory in this case. I give below their main results

Gluon propagator

Dressing function of the ghost propagator

Running coupling

These results confirm completely the decoupling solution. The definition of the running coupling is the one proposed by Alkofer and von Smekal and it is my personal conviction that it conveys the right physical behavior of the theory. This is exactly the scenario I have derived in my paper (see here) that has been published on Physics Letters B too and has arisen a lot of rumors around. You will not find this paper cited in this work as these authors have concerns about gauge invariance in my computations. As you may know from my dispute with Terry Tao, gauge invariance is not a problem here. One could ask why a mathematical technique, like a gradient expansion is, should not work for Yang-Mills equations but it does for all other equations of mathematical physics. Anyhow, I am here ready to listen to whoever is able to prove this. With this proof in hand one should also warn all general relativists that use this technique and put it in their handbooks.

The authors conclude their paper by pointing out weaknesses in lattice computations that may bring in discussion their results. Finally, they ask if the other solution, the one with a scaling behavior, can emerge from lattice computations. The understanding of this question is surely of relevant interest. We stay tuned to hear news about.

Paper replacement

I have updated the paper with the answer to Terry Tao on arxiv (see here). No correction was needed, rather I have added a new result giving the next-to-leading order correction for the Yang-Mills field. This result is important as it shows the right approximate solution, in an expansion into the inverse of the coupling constant, for the mapping between the scalar and the Yang-Mills field. As we repeated a lot of times, Smilga’s solutions are all is needed to work out our argument as this relies on a gradient expansion. A gradient expansion at the leading order has a solution depending just on time variable. But, as this has been a reason for discussion, I have also shown to what extent my approach applies to the solution of the quartic scalar field given in the form

with with an integration constant and the coupling. But I would like to emphasize that the relevance of these solutions for the Yang-Mills case was just demanded by Tao’s criticism but it is not needed for my argument to work. So, the main result of this paper is that

As it has been noted elsewhere, higher order corrections are zero in the Lorenz gauge. This result is certainly not trivial and worth to be considered in a classical analysis of Yang-Mills equations.

Finally, we note as any concern about gauge invariance is just worthless. Smilga’s solutions are exact solutions of the Yang-Mills equations. Casting doubt on them using gauge invariance arguments should be put on the same ground as casting doubt on Kasner solution of Einstein equations using general covariance reasons. Nothing worth to spend time on but a poor excuse to ignore a good work.

PHENIX says gluons are not all the story

PHENIX is a collaboration working with data extracted from RHIC (Relativistic Heavy Ion Collider) located at Brookhaven Labs. In an experiment with proton-antiproton colliding beams and looking at the ejected they were able to extract the contribution of the gluons to the proton spin. They did this using Next-to-Leading-Order perturbation theory fixing the theory scale at . Their paper is here and will appear shortly in Physical Review Letters. Their result is

that is consistent with zero. This is an independent confirmation of the results of the COMPASS Collaboration that we discussed here. These results let us know that in a proton no contribution to the spin comes from glue, rather this is mostly orbital angular momentum. So, why is this conclusion so relevant? From our point of view we know that, in the low energy limit, glue carries no spin. Rather, true excitations of the Yang-Mills field are some kind of colorless states that makes the spectrum and having the lower state with a massive glueball that can also be seen in labs. We know that this state is the resonance. This is the scenario that is emerging from experiments and that whatever theory one can think about should explain.

Update: COMPASS Collaboration confirms small polarization of the gluons inside the nucleon (see here, to appear in Physics Letters B). The current world situation is given in their figure that I put here with their caption (for the refs check their paper).

These results, emerging from several different collaborations, are saying to us a relevant information. Glue seems to carry no spin in the low-energy limit. I think that any sound approach to manage QCD in this case should address this result. The main conclusion to be drawn is that glue excitations seen in this case are different from those seen in the high-energy limit. This is a strong confirmation of our point of view presented here and in published papers. It is a mounting evidence that appears to outline a clear scenario of strong interactions at lower energies.

The question of the conformal solution

There is currently a lot of activity to understand the behavior of the two-point functions in a Yang-Mills theory when quarks are not considered. The relevance of these results relies on the possibility to get working tools to manage low-energy phenomenology of QCD. E.g. we know quite well that the Nambu-Jona-Lasinio model is very successful to describe the behavior of hadronic matter and this model can be easily derived from full QCD if one knows the gluon propagator and the behavior of the ghost field. This idea dates back to a paper by Terry Goldman and Richard Haymaker (see here) on 1981. This can be summed up by saying that: given the gluon propagator one can get back a Nambu-Jona-Lasinio model. One could be able to derive it directly from QCD and this would be a great achievement explaining a lot of work done in several decades by a lot of smart researchers.

In these days it seems that we have to cope with a couple of scenarios and long lasting debate is still alive about them. One of this, the conformal solution, has been supported by a lot of researchers for a long period of time, making sometime very difficult for other scenarios to be commonly accepted and being published on archival journals. The conformal solution is easy to describe with the following sentences:

• The gluon propagator goes to zero at lower momenta.
• The ghost propagator goes to infinity at lower momenta faster than the free case.

Supporters of this solution also claimed that the running coupling reaches a fixed point at zero momenta. This fixed point was strongly lowered as lattice computations easily showed that things do not stay this way.

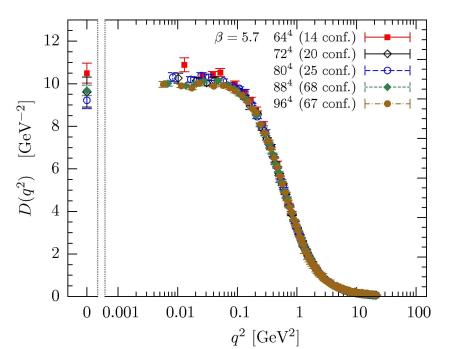
Indeed, lattice computations showed without doubt, increasing the volume, as the gluon propagator reaches a finite value at zero momenta and never converges toward zero. The ghost propagator is seen to behaves exactly as that of a free particle. But notwithstanding such an evidence, much effort is still devoted to understand why the conformal solution is not seen in such computations. A lot of hypotheses were put forward to explain why Yang-Mills propagators do not behave in such a well acquired way.

Axel Maas had a bright idea on this way to understand. He turned his attention to the D=2 model on the lattice (see here). Nobody did this before as this model is known to be trivial as it has no dynamics at all. This was proved by ‘t Hooft long ago. Maas showed that the 2D model on the lattice gives back the conformal solution. This means that a Yang-Mills model without dynamics has two-point functions behaving like those of the conformal solution. Most people saw this as a strong support to the conformal solution but things should be seen the other way round. Removing dynamics makes the conformal solution appear and lattice computations in 3 and 4d, that use the same code, are telling us the right behavior of the two-point functions. This is a serious setback for this approach and my personal view should be that any effort to further support this kind of solution should be  abandoned as is a loss of resources and precious time. But this could be a very difficult choice for a lot of people that for a long time worked on this and contributed to create this scenario.

In my opinion, the most severe drawback of this solution is that it goes against the original idea by Goldman and Haymaker that the gluon propagator should give back the Nambu-Jona-Lasinio model. Indeed, the conformal solution does not even give back a mass gap and it is practically useless to answer to a lot of open questions in the low-energy phenomenology. In some way it remembers to me the position  of the bootstrap model against the gauge paradigm that in the end proved to be the more fruitful approach. The last paper by Cucchieri and Mendes (see here) proves without doubt that the right form is a sum of Yukawa propagators and this gives back immediately a Nambu-Jona-Lasinio model.

As I cannot see reasons for people supporting the conformal solution to surrender, I think a lot of time will pass yet before truth will be acquired. Meantime, we stay here looking at the fight between such  strong contenders.