Regularity in the spectrum of Yang-Mills theory

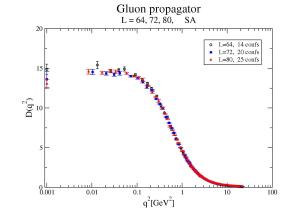
We have seen here that the gluon propagator can be fitted with a Yukawa form that gives a mass gap . The pure number 1.25 fixes the ground state of the theory. Higher excited states in the spectrum will be characterized by a greater pure number multiplying the QCD constant of 440 MeV. The question we ask here is: Are there other lattice computations supporting this view? We show here that this is  indeed the case.

As already pointed out, the spectrum in D=3+1 for Yang-Mills theory, also claimed to be a glueball spectrum, has been computed by Teper et al. and Morningstar et al. But these computations generally give the first few states for each kind of resonance. So to say, one has just and and this may not be too convincing. But there is a paper on arxiv due to Harvey Meyer, that worked with Teper’s Group in Cambridge,  that extends the computations further (see here). This is unpublished material being a PhD thesis.

We can sum up the pure numbers obtained by Meyer for the case with the relative error:

Now we assume that this spectrum has the simple form of an harmonic oscillator, that is we take . Our aim will be to obtain in close agreement with computations for the gluon propagator. We obtain the following table

There is a lot to say about this result. It is striking indeed! We get practically the same as the one obtained from lattice computations of the gluon propagator that, as said above was 1.25, if we consider that the error increases with . But what is more, one can extrapolate the above results to obtaining the proper ground state of the theory again recognizing the resonance. We just note that if we use the improved values 3.55(7) and 5.69(10) by Teper et al. (see here) we get a still better agreement obtaining 1.183 with an error of 0.023 and 1.14 and error of 0.05, making very near the value 1.19 that we claimed would give an improved spectrum in AdS/CFT computations (see here).

This computation makes clear a point. Present lattice computations of the glueball spectrum are not fully satisfactory for D=3+1 as they do not seem to hit the right ground state of the theory as is done by lattice computations for the propagators. I think some improvement is needed here for a better understanding of the situation.

We will have more to say about Yang-Mills spectrum in future posts.

 

How far are we from a proof of existence of the mass gap?

A well acquired fact is that there are seven problems that will be awarded with a rich prize by the Clay Institute (see here). One of these problems touch us that work on QCD very near. This is the question of the existence of a mass gap for a Yang-Mills theory (see here). I would like to emphasize that Clay Institute is a mathematical institution and, as such, it is acquired that a proof given by a physicist could not be enough to satisfy the criteria of professional mathematicians to be called a proof. Anyhow, one can always suppose that a sound mathematical idea due to some physicists can be made rigorous enough by the proper intervention of a mathematician. But this last passage is generally neither that simple nor obtainable in a short time.

As we have discussed here, present lattice results are already enough to have given to physicists a sound proof of the existence of a mass gap for a Yang-Mills theory in D=3+1. In this post I will avoid to discuss about theoretical work in D=3+1 but rather I would like to point out some relevant work appeared for the case D=2+1. In this case there are two categories of papers to be considered. The first category corresponds to the works of Bruce McKellar and Jesse Carlsson. These works are largely pioneering. In these papers the authors consider the theory on the lattice and try to solve it through analytical means (here, here and here appeared in archival journals). They reached a relevant conclusion:

The spectrum of the Yang-Mills theory in D=2+1 is that of an harmonic oscillator.

This conclusion should be compared with the results in D=3+1 on the lattice. We have seen here that looking in a straightforward way to these computations one arrives easily to the conclusion that the theory is trivial. Yes, it has a mass gap but is trivial. The only missing block is the spectrum. So, Carlsson and McKellar give us the missing step. Also the spectrum is consistent with the view that the theory is trivial.

Then we look at the second category of papers. These papers arose from an ingenious idea due to Kim, Karabali and Nair (e.g. see here) that introduced the right variables to manage the theory. In this way one reduces the problem to the one of diagonalizing a Hamiltonian obtaining eigenstates and eigenvalues. Building on this work, Leigh, Minic and Yelnikov were able to postulate a new nontrivial form of the ground state wavefunctional producing the spectrum of the theory in D=2+1 in closed analytical form (see here and here). The spectrum was given as the zeros of Bessel functions that in some approximation can be written as that of an harmonic oscillator. The open problem with this latter approach relies on the proof of existence of the postulated wavefunctional. This may not be easy.

The conclusion to be drawn from this is that we have already sound evidences that a mass gap for Yang-Mills theory exists. These proofs could not be satisfactory for a mathematician but surely for us physicists give a solid ground to work on.

A note about AdS/CFT and Yang-Mills spectrum

There is a lot of activity about using this AdS/CFT symmetry devised in the string theory context to obtain the spectrum of a pure Yang-Mills theory in D=3+1. To have an idea about one can read here. The essential point about this approach is that it does not permit the computation of the mass gap. Rather, when given the ground state value as an input, it should be able to obtain all the spectrum. I should say that current results are indeed satisfactory and this approach is worthing further pursuing.

Apart from this, we have seen here that the ground state, as derived using the lattice computations of the gluon propagator, is quite different from current results for the spectrum as given here and here. Indeed, from the gluon propagator, fixing the QCD constant at 440 MeV, we get the ground state at 1.25. Teper et al. get 3.55(7) and Morningstar et al (that fix the constant at 410 MeV) get about 4.16(11). Morningstar et al use an anisotropic lattice and this approach has been problematic in computations for the gluon propagator ( see the works by Oliveira and Silva about) producing disagreement with all others research groups or, at best, a lot of ambiguities. In any case we note a large difference between propagator and spectrum computations for the ground state. This is a crucial point.

Experiments see f0(600) or . Propagator computations see f0(600) and but spectrum computations do not. Here there is a point to be clarified between these different computations about Yang-Mills theory. Is it a problem with lattice spacing? In any case we have a discrepancy to be understood.

Waiting for an answer to this dilemma, it would be interesting for people working on AdS/CFT to lower the input ground state assuming the one at 1.25 (better would be 1.19 but we will see this in future posts) and then checking what kind of understanding is obtained. E.g. is the state at 3.55 or 4.16 recovered? Besides, it would be nice to verify if some kind of regularity is recovered from the spectrum computed in this way.

A nice paper

Today in arxiv a new paper appeared by Dudal, Gracey, Sorella, Vandersickel and Verschelde here. This is a cooperation between Universities in Belgium, UK and Brazil. These authors have found a way to keep alive the Gribov-Zwanziger scenario by working out an extended Yang-Mills Lagrangian. Indeed, by taking into account the recent lattice results, these authors modify Yang-Mills Lagrangian to be consistent with them by adding meaningful terms that maintain renormalizability and prove that in this way the Gribov-Zwanziger scenario survives.

This work is a continuation of other interesting works by the same authors. The only point to be emphasized is that in this case we lose a minimality criterion that would imply the formation of a mass gap through the dynamics of the theory itself. This latter point seems the one supported by lattice computations as we discussed here. 

Meaning of lattice results for the gluon propagator

We have shown the results of the lattice computations of the gluon propagator here. It would be important to get an understanding of what is going on in the low momentum limit. Indeed, this is not impossible but rather very easy. The reason for this relies on the fact that we assume that a mass gap forms in the limit of low momenta explaining the short range proper to nuclear forces. But there is more to say. This mass gap must represent an observable resonance in the spectrum of the light scalar mesons. We expect this as Yang-Mills theory is the one describing nuclear forces and if this theory is the true one, apart mixing with quarks states, its spectrum must be observed in nature.

In order to pursue our aims we consider the data coming from Attilio Cucchieri and Teresa Mendes being those for the largest volume here. If there is a mass gap the simplest form of propagator to use (in Euclidean metric) is the Yukawa one

being a constant and the mass gap entering into the fit. We obtain the following figure

for and . This result is really shocking. The reason is that a resonance with this mass has been indeed observed. This is f0(600) or and recent analysis by S. Narison, W. Ochs and others ( see here and here) and chiral perturbation theory as well (see here or here) have shown that this resonance has indeed a large gluonic content. But this is not enough.

If we assume that the computation by Cucchieri and Mendes used a QCD constant of about 440 MeV we can take the ratio with the mass gap to obtain an adimensional number of about 1.25. But for the QCD constant, that should be fixed in any computation on the lattice, there is no general agreement about and this constant should be obtained from experimental data. When one is able to solve Yang-Mills theory by analytical means this constant is an integration constant arising from the conformal invariance of the theory. The other value that is generally chosen by lattice groups is 410 MeV. This would give a mass gap of about 512 Mev that is very near the value obtained from experimental data ( e.g. see here).

So, the conclusions to be drawn from lattice computations are really striking. We have seen that the ghost behaves like a free particle, i.e. decouples from the gluon field. On the same ground it is also seen that lowering momenta makes the running coupling going to zero. Together with a fit to a Yukawa propagator we recognize here all the chrisms of a trivial theory! The same that is believed to happen to scalar field theory in the same limit in four dimensions.

Indeed, this is not all the story. The spectrum of a Yang-Mills theory is more complex and higher excitations than are expected. We will discuss this in the future and we will see how to recover the spectrum of light scalar mesons, at least for the gluonic part, without losing the property of triviality proper to the theory.

Strong perturbation theory

In another post we have defined what a strongly perturbed physical system is. This implied that we know how to do strong perturbation theory, that is, one takes her preferred differential equation and get a solution series for the case of a large parameter. We show here that is indeed the case. So, let us consider as an example the following differential equation:

.

We know the exact solution of this equation being

to be compared to our approximated ones. The weak perturbation case, , asking for a solution in the form

gives the set of equations

and finally

and from the numerical comparison for we get the curves

that is really satisfactory. We now look for a solution series in the form

but a direct substitution into the original equation gives nonsense. There is one more step to do and this is a rescaling in time, that is we use instead of the scaled variable . After this substitution is accomplished we can put the strong perturbation series into the equation and obtain the meaningful set of differential equations

where now “dot” means derivation with respect to . We have finally the solution series, undoing the rescaling in time,

Numerical comparison with gives

that is almost perfect in the coincidence between the exact and the approximate case. The method indeed works!

We note the following:

• From the set of equations of the strong perturbation case we note that we have just interchanged the perturbation with respect to the weak perturbation case to obtain the series with inverted expansion parameter. This serves just as a bookeeper but it is not needed. This is duality in perturbation theory (look here and here). 
• The strong perturbation series is a series in small times. Indeed the time scale is set by that decides how far can we go into the time scale for the comparison.

It is just curious that no mathematician in the history was able to get such a method out understanding that it was just a rescaling of the independent variable away. I was lucky as this did not happen!

So, as said at the start, you can take your preferred differential equation and sort out a solution series in a regime you have never seen before.

Have fun!

Gluon and ghost propagators on the lattice

For a true understanding of QCDat low energies we need to know in a clear way the behavior of the gluon and ghost propagators in this limit. This should permit to elucidate the general confinement mechanism of a Yang-Mills theory in the strong coupling limit. Things are made still more interesting if this comprehension should imply a dynamical mechanism for the generation of mass. The appearance of a mass in a otherwise massless theory gives rise to the so-called “mass gap” that should appear in a Yang-Mills theory to explain the short range behavior of the strong force.

A lot of computational effort has been devoted to this task mainly due to three research groups in Brazil, Germany and Australia. These authors aimed to reach larger volumes on the lattice as some theoreticians claimed loudly that finite volume effects was entering in these lattice results. This because all the previous theoretical research using the so called “functional methods”, meaning in this way the solution of Dyson-Schwinger equations in some approximation, pointed toward a gluon propagator going to zero at low momenta, a ghost propagator going to infinity faster than the free case and the running coupling (defined in some way) reaching a fixed point in the same limit. These theoretical results support views about confinement named Gribov-Zwanziger and Kugo-Ojima scenarios after the authors that proposed them.

Two points should be emphasized. The idea that the running coupling in the infrared should go to a fixed point is a recurrent prejudice in literature that has no theoretical support. The introduction of a new approach to solve the Dyson-Schwinger equations by Alkofer and von Smekal supported this view and  the confinement scenarios that were implied in this way. These scenarios need the gluon propagator going to zero. But these authors are unable to derive any mass gap in their theory and so we have no glueball spectrum to compare with experiment and other lattice computations. Anyhow, this view has been behind all the research on the lattice that was accomplished in the last ten years and whatever computation was done on the lattice, the gluon propagator refused to go to zero and the running coupling never reached a fixed point.

It should be said that some voices out of the chorus indeed there are. These are mainly the group of Philippe Boucaud in France and some numerical works on Dyson-Schwinger equations due to Natale and Aguilar in Brazil. These authors were able to describe the proper physical situation as appears today on lattice but they met difficulties due to skepticism and prejudices about their work due to the mainstream view described above. Since 2005 I proposed a theoretical approach that fully accounts for these results and so I just entered into the club of some heretical view! I will talk of this in my future posts.

After the Lattice 2007 Conference (for the proceedings see here) people working on lattice decided to not pursue further increasing volumes as now an agreement is reached on the behavior of the propagators. This view is at odds with functional methods and no precise understanding exists about why things are so. Some results in two dimensions agree with functionalmethods but the theory is known to be trivial in this case (there is a classical paper by ‘t Hooft about). To give you an idea of the situation I have put the following lattice results at here, here and   here respectively:

 and finally

Then we can sum up the understanding obtained from the lattice about Yang-Mills theory:

• Gluon propagator reaches to finite value at low momenta.
• Ghost propagator is that of a free particle.
• Running coupling, using the definition of Alkofer and von Smekal, goes to zero at low momenta.

These results agree perfectly with the ones obtained by Boucaud et al., Aguilar and Natale and myself. In a future post we will discuss the way these lattice results seem to give a consistent view with current phenomenology of light scalar mesons.

When is a physical system strongly perturbed?

Generally speaking, a physical system is described by a set of differential equations whose solution is given by a state variable . So, one has . The solution of this set of differential equations gives all one needs to obtain observables, that is numbers, to be compared with experiments. When the physical system undergoes the effect of a perturbation the problem to be solved is

and we say that perturbation is small (or weak) as we consider the limit .  In this case we look for a solution series in the form

.

The case of a strong perturbation is then easily obtained. We say that a physical system is strongly perturbed when the limit is considered and the solution series we look for has the form

.

We will see that this solution series can generally be built and can be obtained by a “duality principle” in perturbation theory arising from the freedom that exists in the choice of what is the perturbation and what is left unperturbed.

A World of Physics and a lot more

This is the start-up post of this new physics blog. I will talk about a lot of questions I care about, mostly current research open problems that need some tribune to be heard. But I will also discuss some other arguments that could be of interest to a larger audience.

Most of the questions on physics that pass to the media are about string theory, unification, quantum gravity and all other aspects of fundamental research that can hit the interest of common people. But one should consider that most of the breakthroughs that happened in science have come from unexpected directions.  And last but not least, there is generally an average time, that is not short, before an important finding becomes a recognized and acquired truth. This means that is important to make knowledge to flow as fastly as possible and blogs are an excellent way to achieve such a goal.

I am working mostly on QCD and for this particular field there are different alleys that are currently pursued and just now something is going to converge for experiments, lattice and theory and is worthwhile to let everybody know the work of these people that someday could impact in a more generally way to all the community. The reason to expect this relies on the fact that QCD is a theory eminently not perturbative and a lot of innovative views should be expected here.

Indeed, one of the most serious problems to face in physics is the treatment of problems where a large parameter enters that makes the problem non perturbative, that is, impossible to manage with perturbation theory. Till now, perturbation theory appears as the only serious approach to get analytical solutions to equations and needs a small parameter to work. Despite several important attempts as the renormalization group and a few of exact solutions, in the end of the day one has to rely on this venerable approach to extract physically meaningful results from equations.

This approach has become such a part of physics that a lot of prejudices invaded some fields where it applies. A clear example of this is quantum field theory. Quantum field theory works only through small perturbation theory and so, renormalization that was born with it is believed to be inherent to any quantum field theory independently on the method one use to treat it. But this latter point of view is to be proved!

So, let us begin. Happy blogging!