Running coupling and Yang-Mills theory

Forefront research, during its natural evolution, produces some potential cornerstones that, at the end of the game, can prove to be plainly wrong. When one of these cornerstones happens to form, even if no sound confirmation at hand is available, it can make life of researchers really hard. It can be hard time to get papers published when an opposite thesis is supported. All this without any certainty of this cornerstone being a truth. You can ask to all people that at the beginning proposed the now dubbed “decoupling solution” for propagators of Yang-Mills theory in the Landau gauge and all of them will tell you how difficult was to get their papers go through in the peer-review system. The solution that at that moment was generally believed the right one, the now dubbed “scaling solution”, convinced a large part of the community that it was the one of choice. All this without any strong support from experiment, lattice or a rigorous mathematical derivation. This kind of behavior is quite old in a scientific community and never changed since the very beginning of science. Generally, if one is lucky enough things go straight and scientific truth is rapidly acquired otherwise this behavior produces delays and impediments for respectable researchers and a serious difficulty to get an understanding of the solution of  a fundamental question.

Maybe, the most famous case of this kind of behavior was with the discovery by Tsung-Dao Lee and Chen-Ning Yang of parity violation in weak interactions on 1956. At that time, it was generally believed that parity should have been an untouchable principle of physics. Who believed so was proven wrong shortly after Lee and Yang’s paper. For the propagators in the Landau gauge in a Yang-Mills theory, recent lattice computations to huge volumes showed that the scaling solution never appears at dimensions greater than two. Rather, the right scenario seems to be provided by the decoupling solution. In this scenario, the gluon propagator is a Yukawa-like propagator in deep infrared or a sum of them. There is a very compelling reason to have such a kind of propagators in a strongly coupled regime and the reason is that the low energy limit recovers a Nambu-Jona-Lasinio model that provides a very fine description of strong interactions at lower energies.

From a physical standpoint, what does it mean a Yukawa or a sum of Yukawa propagators? This has a dramatic meaning for the running coupling: The theory is just trivial in the infrared limit. The decoupling solution just says this as emerged from lattice computations (see here)

What really matters here is the way one defines the running coupling in the deep infrared. This definition must be consistent. Indeed, one can think of a different definition (see here) working things out using instantons and one see the following

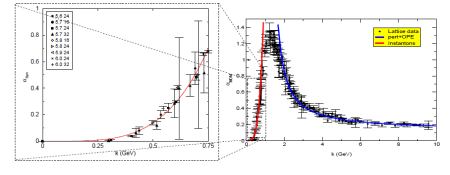One can see that, independently from the definition, the coupling runs to zero in the deep infrared marking the property of a trivial theory. This idea appears currently difficult to digest by the community as a conventional wisdom formed that Yang-Mills theory should have a non-trivial fixed point in the infrared limit. There is no evidence whatsoever for this and Nature does not provide any example of pure Yang-Mills theory that appears always interacting with Fermions instead. Lattice data say the contrary as we have seen but a general belief  is enough to make hard the life of researchers trying to pursue such a view. It is interesting to note that some theoretical frameworks need a non-trivial infrared fixed point for Yang-Mills theory otherwise they will crumble down.

But from a theoretical standpoint, what is the right approach to derive the behavior of the running coupling for a Yang-Mills theory? The answer is quite straightforward: Any consistent theoretical framework for Yang-Mills theory should be able to get the beta function in the deep infrared. From beta function one has immediately the right behavior of the running coupling. But in order to get it, one should be able to work out the Callan-Symanzik equation for the gluon propagator. So far, this is explicitly given in my papers (see here and refs. therein) as I am able to obtain the behavior of the mass gap as a function of the coupling. The relation between the mass gap and the coupling produces the scaling of the beta function in the Callan-Symanzik equation. Any serious attempt to understand Yang-Mills theory in the low-energy limit should provide this connection. Otherwise it is not mathematics but just heuristic with a lot of parameters to be fixed.

The final consideration after this discussion is that conventional wisdom in science should be always challenged when no sound foundations are given for it to hold. In a review process, as an editorial practice, referees should be asked to check this before to kill good works on shaky grounds.

I. L. Bogolubsky, E. -M. Ilgenfritz, M. Müller-Preussker, & A. Sternbeck (2009). Lattice gluodynamics computation of Landau-gauge Green’s functions in the deep infrared Phys.Lett.B676:69-73,2009 arXiv: 0901.0736v3

Ph. Boucaud, F. De Soto, A. Le Yaouanc, J. P. Leroy, J. Micheli, H. Moutarde, O. Pène, & J. Rodríguez-Quintero (2002). The strong coupling constant at small momentum as an instanton detector JHEP 0304:005,2003 arXiv: hep-ph/0212192v1

Marco Frasca (2010). Mapping theorem and Green functions in Yang-Mills theory PoS FacesQCD:039,2010 arXiv: 1011.3643v3

H->WW channel at ATLAS

Today is started Higgs Hunting conference at Orsay (France). Data for WW decay of Higgs boson from ATLAS have been made public. The talk is here. The data provide a clear excess in this channel and the rate is somewhat higher with respect to the Standard Model expectations of times. Gamma-Gamma channel remains the one going far better with respect possible clues of beyond standard model physics.

Of course, these are too feeble clues yet and may result into flukes turning Higgs boson of Standard Model the best fit for the data. Our hope is that further analysis will confirm these excesses.

Quote of the day

“So far, the h particle does indeed walk and quack very much like a Higgs boson.”

John Ellis and Tevong You 

QCD 12 and Higgs’ tears

I have spent this week in Montpellier being a participant to QCD 12, a biannual conference organized by Stephan Narison. It is the third time that I go to Montpellier for this conference and there are always very good reasons for being there. Essentially, the quality of physics and beauty of the city are already worthwhile and sound arguments but also the excellent organization  by the host and the attention reserved to the guests are not the least. This year we have had the blessing of a historical event in physics: The discovery at CERN of the Higgs particle. Stephan organized the event with the webcast from CERN the first two hours on Wednesday and so we heard directly from Gianotti and Incandela what they were seeing at LHC.  The conference is a fair interplay between experiment and theory in a field, QCD, that is very active and with several important open problems. Maybe, we would like to emphasize that is QCD that gives mass to everyday things, and not the Higgs boson, and this means that the solution of the mass gap problem and the developing of proper methods to manage non-perturbative regimes are essential to the understanding of our common perception of reality. Indeed, Roberto Mussa of University of Turin remembered us an argument that  makes Higgs boson essential to everyday life: The stability of matter. Without the Higgs boson quarks would have equal masses and so, proton would decay into neutron. The difference in mass between u and d quarks is essential and this originates from Higgs boson.

In this conference several questions emerged that were absolutely exciting. Hadron spectrum is not so well understood both in the low and high part. There is a plenty of experimental results claiming for an explanation. Labs keep on finding resonances that have not an immediate explanation and make hard the life of us theoreticians. One should compare the situation with the case of electromagnetic interactions where a Rydberg formula was promptly found and understanding of bound states is now quite straightforward. For hadrons we have hard times already to catch what the structure of a resonance is. These difficulties arise from the missing of technique to manage non-perturbative problems in a way similar to the weak coupling limit. Indeed, on Wednesday, some approaches were given to manage this kind of situation and, besides my talk, the most common technique is AdS/QCD starting from Maldacena conjecture. This was also the argument of Stefano Nicotri and Floriana Giannuzzi. They are students of Pietro Colangelo and contributed to the organization of Lecce conference. I have spent a lot of good time with them and so we exchanged a lot of opinions about this matter. On this line, Hans Günter Dosch put all us down showing that the situation with this approach is not so fine. Simply, it appears like a proper model for the mapping between gravity and QCD is lacking yet but, of course, people is actively pursuing it.

A talk that gave me some interesting views was the one by Kenichi Konishi. He pointed out how the confinement can emerge looking at the behavior of the supersymmetric counterpart of Yang-Mills theory. He pointed out the problems with the idea of monopoles, already discussed by Kei-Ichi Kondo at Lecce. And you bet, when one looks at SYM one recover the condensation of a scalar field! Konishi works at University of Pisa where teaches quantum mechanics.

On the line of non-perturbative approaches were the talks by Matteo Giordano and Enrico Meggiolaro. They are trying to re-derive from first principles the Froissart bound. This is a bound on hadronic scattering that can be obtained just using unitarity and dispersion relations. This bound depends crucially on the mass gap of the theory and so, again, we are coping with all the problems given above. Meggiolaro showed that, using lattice computations, the limit can be recovered with the proper constant while Matteo is approaching this problem using AdS/QCD. With Matteo we meet again in Montpellier after four years. We remembered each other immediately and drunk a last beer before leaving on Friday night after the social dinner, with Montpellier streets full of people and pleasant noise.

A talk that I followed with a lot of interest was the one given by Pietro Falgari. He is working on the use of perturbation theory at high-energy in QCD to evaluate the production rate of pairs of top quarks. Even if in this limit perturbation theory can be applied in QCD, they have difficulties mostly related to resum a quite singular series with logarithmic contributions. So, also when perturbation theory applies, QCD does not save us from problems. With Pietro I have spent a lot of time in Montpellier and we left the city together on Saturday with the same flight.

An interesting talk was the one given by Eduardo de Rafael about the determination of the g factor of the muon. This is a truly relevant matter as this measurement can give a clue to new physics. But, as de Rafael pointed out, the critical point is the determination of the hadronic contribution. Presently, there is a 3.6 sigmas discrepancy between the theoretical computed value and the measured one. We cannot be confident that the evaluation of the hadronic part is not correctly accomplished.

Last but not least, the current work of Narison on heavy flavors with sum rules. This approach is now fairly well stable and provides results also better than other non-perturbative techniques. This has been shown in the talk by his collaborator Albuquerque from Sao Paolo. Of course, results like these should be a reference for experiments much in the same way are others as lattice computations. Finally, I would like to cite the talk by Robert Kaminski. He presented the fine work done in collaboration with R. Garcia-Martin J. R. Pelaez, J. Ruiz de Elvira aimed to a precise determination of the properties of f0(600) and f0(980). Their results are striking indeed as they fix very precise values to the mass and width of these resonances, in close agreement with preceding works. It is my personal conviction that a serious theoretical approach should be derive both the mass and the width of these resonances deriving at the same time their structure.

Wednesday was the great day. There was a lot of expectation and the great discovery was in the air predated by a lot of rumors here and there. Our organizers did a great work both providing the webcast from CERN and with a pair of talks on Friday from people of CMS and ATLAS. There has been a religious silence during the talks of Incandela and Gianotti just interrupted by applause at the announcements of the 5 sigmas discovery by the two groups. Following this, we discussed a lot about this matter and, besides it is very standard model-like this particle at the moment, we all were very cautious to claim supersymmetry dead. Rather we would like to know more about the rates in the various channels, results to be known in the near future in order to answer the question put forward by CERN director Rolf-Dieter Heuer: Which one? A girl at my conference asked for other four Higgs and we all know why. Talking with a colleague at ATLAS here in Montpellier, he told me a quite interesting figure for the WW channel but I will not disclose it. Work is in progress yet and data are really too fresh to be discussed. It is a matter of few months and we will know better about the nature of this new particle. Meanwhile, I would like to remember Higgs’ tears after the great announcement and the handshaking with Fabiola Gianotti, after the splendid talk by her, confirming the expectation of almost fifty years of waiting with hopes often not coming up. It is an achievement that very few scientists can claim in their lifetime. The same must apply identically to Englert, Brout, Guralnik, Hagen, and Kibble.

On Friday, the program was concluded by the talks of people from CERN, on behalf of ATLAS and CMS Collaborations. Pushpa Bhat from Fermilab talked on behalf of CMS Experiment while Robert Harrington from Particle Physics Experimental Group of University of Edinburgh talked on behalf of ATLAS Experiment. This was a great conclusion for the Conference, hearing directly from people at CERN, about the great achievement announced on Wednesday.

As a final remark, I would like to thank all people with whom I shared beautiful moments at this conference. Besides people I have already mentioned, I would like to thank Stefano Venditti, Antonio Cassese, Andrey Tayduganov, Federico Mescia, Benjamin Obherof. A great thank goes to Stephan Narison for giving me the chance to give a talk here, for giving me the chance to be chairman for the first time, and for the excellent and really enjoying organization in a beautiful city. See you again!

Update: Talks can be downloaded here.

Higgs particle finally found!

After a two hours seminar, both CMS and ATLAS spokepersons confirmed a 5 sigmas discovery of a new particle that is consistent with the Higgs particle of the Standard Model. The mass is in agreement with previous clues on last December seminar from CERN: About 125 GeV for both experiments.

Congratulations for the great discovery to all people participating to this succesful effort!