Unpublishable

I tried in different ways to get this paper through the community with standard channels. As far as I can tell, this paper is unpublishable. By this I mean that journals not even send it to referees to start a normal review process or all people try to stop it from making it known. The argument is always the same: A reformulation of quantum mechanics using stochastic processes but using noncommutative geometry this time. I apologize to the community if this unacceptable approach has bothered people around the World but this is the fate of some ideas. Of course, if somebody has the courage and the willing to publish, let me know and I will appreciate the tentative with infinite gratefulness.

Now, back to sane QCD.

Happy new year!

Quantum gravity

Quantum gravity appears today as the Holy Grail of physics. This is so far detached from any possible experimental result but with a lot of attentions from truly remarkable people anyway. In some sense, if a physicist would like to know in her lifetime if her speculations are worth a Nobel prize, better to work elsewhere. Anyhow, we are curious people and we would like to know how does the machinery of space-time work this because to have an engineering of space-time would make do to our civilization a significant leap beyond.

A fine recount of the current theoretical proposals has been rapidly presented by Ethan Siegel in his blog. It is interesting to notice that the two most prominent proposals, string theory and loop quantum gravity, share the same difficulty: They are not able to recover the low-energy limit. For string theory this is a severe drawback as here people ask for a fully unified theory of all the interactions. Loop quantum gravity is more limited in scope and so, one can think to fix the problem in a near future. But of all the proposals Siegel is considering, he is missing the most promising one: Non-commutative geometry. This mathematical idea is due to Alain Connes and earned him a Fields medal. So far, this is the only mathematical framework from which one can rederive the full Standard Model with all its particle content properly coupled to the Einstein’s general relativity. This formulation works with a classical gravitational field and so, one can possibly ask where quantized gravity could come out. Indeed, quite recently, Connes, Chamseddine and Mukhanov (see here and here), were able to show that, in the context of non-commutative geometry, a Riemannian manifold results quantized in unitary volumes of two kind of spheres. The reason why there are two kind of unitary volumes is due to the need to have a charge conjugation operator and this implies that these volumes yield the units 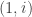in the spectrum. This provides the foundations for a future quantum gravity that is fully consistent from the start: The reason is that non-commutative geometry generates renormalizable theories!

The reason for my interest in non-commutative geometry arises exactly from this. Two years ago, I, Alfonso Farina and Matteo Sedehi obtained a publication about the possibility that a complex stochastic process is at the foundations of quantum mechanics (see here and here). We described such a process like the square root of a Brownian motion and so, a Bernoulli process appeared producing the factor 1 or i depending on the sign of the steps of the Brownian motion. This seemed to generate some deep understanding about space-time. Indeed, the work by Connes, Chamseddine and Mukhanov has that understanding and what appeared like a square root process of a Brownian motion today is just the motion of a particle on a non-commutative manifold. Here one has simply a combination of a Clifford algebra, that of Dirac’s matrices, a Wiener process and the Bernoulli process representing the scattering between these randomly distributed quantized volumes. Quantum mechanics is so fundamental that its derivation from a geometrical structure with added some mathematics from stochastic processes makes a case for non-commutative geometry as a serious proposal for quantum gravity.

I hope to give an account of this deep connection in a near future. This appears a rather exciting new avenue to pursue.

Ali H. Chamseddine, Alain Connes, & Viatcheslav Mukhanov (2014). Quanta of Geometry: Noncommutative Aspects Phys. Rev. Lett. 114 (2015) 9, 091302 arXiv: 1409.2471v4

Ali H. Chamseddine, Alain Connes, & Viatcheslav Mukhanov (2014). Geometry and the Quantum: Basics JHEP 12 (2014) 098 arXiv: 1411.0977v1

Farina, A., Frasca, M., & Sedehi, M. (2013). Solving Schrödinger equation via Tartaglia/Pascal triangle: a possible link between stochastic processing and quantum mechanics Signal, Image and Video Processing, 8 (1), 27-37 DOI: 10.1007/s11760-013-0473-y

News from CERN

Two days ago, CERN presented their new results at 13 TeV to the World. Of course, collected data so far are not enough for conclusive results but the these are exciting anyway. The reason is that both the collaborations, CMS and ATLAS, see a bump at around 750 GeV in the decay. Summing up the results of the two collaborations, they are around without look elsewhere effect, not yet a discovery but, probably, at the summer conferences they will have something more conclusive to say. This could be an unlucky fluctuation but this situation remember us the story of the discovery of the Higgs boson more than three years ago. The question if this is beyond Standard Model physics is what I will try to answer in these few lines.

Firstly, if this particle is real, it decays with two photons exactly as the Higgs boson. Secondly, with a final state like this it can have only spin 0 or 2. We will be conservative and assume that this is not a graviton. Rather, it is a sibling of the Higgs particle. Besides, it was not observed in run I but is not inconsistent with data from there. It appears like the increased luminosity favored its appearance. We want to be more conservative and we take for granted just the Lagrangian of the Standard Model. So, what is this beast?

My answer is that this could be an excited state of the Higgs boson that, having a production rate lower than its ground state seen at run I, needed more luminosity to be observed. You do not need to change the Lagrangian of the Standard Model for this and it is not BSM physics yet. You do not even need a technicolor theory to describe it. The reason is that the Higgs part of the Standard Model can be treated mathematically yielding exact solutions. The quantum field theory can be exactly solved and the spectrum of the theory says exactly what I stated above (see here, and here). The Higgs model per se is exactly solvable. So, Jester’s idea to add another scalar field to the Lagrangian model is useless, it is all just inside and you will get a two photon final state as well.

Of course, it is too early to draw a final conclusion and a wealth of papers with a prompt explanation flooded arxiv in these two days. With the restart of LHC on spring and the collecting of more data, things will be clearer than now. For the moment, this hint is enough to keep us excited for the next few months.

Marco Frasca (2015). A theorem on the Higgs sector of the Standard Model arxiv arXiv: 1504.02299v2

Marco Frasca (2015). Quantum Yang-Mills field theory arxiv arXiv: 1509.05292v1