After the satisfactory derivation of the bottomonium ground state mass (see here) we would like to apply similar concepts to charmonium. Before we go on I would like to mention here the beautiful paper by Nora Brambilla and a lot of other contributors that any serious researcher in the field of heavy quark physics should read (see here). This paper has been published as a yellow report by CERN. What we want to prove here is that the knowledge of the gluon propagator can give a nice understanding of the ground state of quarkonia. Anyhow, for charmonium we could not be that lucky as relativistic effects are more important here than for bottomonium. Besides, if we would like to expand to higher order in r the quark potential we would be no more able to treat the Schroedinger equation unless we treat these terms as a perturbation but this approach is not successful giving at best slowing convergence of the series for bottomonium and an useless result for charmonium.
PDG gives us the data for the ground state of charmonium 
and then, our computation gives
that has an error of about 13%. With a quark mass of 1.44 GeV we would get a perfect agreement with
As said at the start, heavy quarkonia are a well studied matter and whoever interested to deepen the argument should read the yellow report by Brambilla and others.
Update:I would like to point out the paper by Stephan Narison (see here and here) that obtains the pole masses of c and b quarks being these the ones I use to obtain the right ground state of charmonium and bottomonium. Striking indeed!
The Gauge Connection 
Hmm perhaps you could try a theoretical post about why we are still unable to tell anything about pions and kaons.
Also I would enjoy if you were able to calculate half-lifes. Remember the empirical rule for half lives of ground states of neutral particles, which I told in Dorigo’s guestposter session.
Alejandro,
That is a good subject for a blog post. My (limited) understanding is that the reason that formulas only work for heavy quark mesons is that the heavy quarks can get so close to one another that they are asymptotically free. This means that the color force can be ignored. Then the reaction becomes an electric attraction, which does not become asymptotically free, and the mesons can be analyzed that way. The formulas fail at higher n because the distance increases, and color forces become too important.
I’m busily thinking about how the concept of asymptotic freedom interacts with the Koide formula you’re familiar with. I’ve got some ideas, but nothing unembarassing.
Alejandro,
The reason why things go so straight for heavy quarks is that a small distance approximation does hold and you get a Coulomb-like potential. Besides, a non-relativistic approximation applies. These facts were all well-known just after the discover of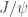
resonance. What I get here is a correction to such a Coulomb-like potential arising from the gluon propagator that fits the bill very well to recover the ground state of such heavy quarkonia. So, Carl’s explanation is fine.
Anyhow, If I could be able to solve Dirac equation with the potential I give, masses of light mesons should come out. I am thinking about this but I also know that a Nambu-Jona-Lasinio model does the job better (see my recent paper http://arxiv.org/abs/0803.0319) than any other kind of approximation as happens instead for heavy quarks.
Then, from a NJL model one should compute half-life. The case I consider for heavy quarkonia reduces to the computation of the eigenvalues of Schroedinger equation and these states do not decay as also happens to hydrogen atom.
Marco