After the acceptance of my paper (see here) I wondered what should have been Smilga’s choice for the SU(3) given its existence. Let me explain what a Smilga’s choice is. Firstly I point out his beatiful book about QCD that was my starting point for all this matter (see here). You will find in this book, in the chapter about classical solutions, that when one chooses a set of values different from zero of the components of the Yang-Mills potential and take these non-null components all equal one gets for space-homogeneous Yang-Mills equations the motion equation of a massless anharmonic oscillator. Smilga asked in the book what the physical meaning of such homogeneous solutions should be. I answered to this smart question with a mapping theorem (take a look at my paper here): Anytime a Smilga’s choice is done one has mapped a solution of the classical Yang-Mills equations onto a solution of a quartic massless scalar field. This result is extremely important as we obtain in this way both the physical meaning of such solutions and a set of classical solutions to do perturbation theory without recurring to some small parameter. Indeed, we know how to manage a quantum scalar field in the strong coupling limit (see here and here).
Now, for SU(2) it is very easy to do a choice that reaches our aim: One takes
and you are done. I have not exploited all the phase space in this case as one should consider that Smilga’s choice is not unique and things get worse as the gauge group is taken more complex. For SU(3) things are really horrible as one has to explore a very large phase space and the product of the structure constants of the group does not admit a simple expression. So, I reduced myself to write down a few lines of code both in C and matlab working out such a product of structure constants. My PC worked fine for me and obtained a lot of results. As said above Smilga’s choice is not unique and one can have a huge number of choices increasing the number of structure constants of the group. So, e.g. the following Smilga’s choice is good for SU(3) leaving you with the right ‘t Hooft coupling in the mapped scalar field
This Smilga’s choice gives a multiplicative overall factor 2 to the scalar field action. Smilga’s choice for SU(2) will leave a factor -3. Of course, these factors will depend on the gauge group but one can ask a couple of mathematical questions that are worth exploring. Firstly, whatever Smilga’s choice one takes that grants the correct ‘t Hooft coupling in the Lagrangian of the scalar field, is the overall factor always the same? Better, does a Smilga’s choice exist that grants for any SU(N) group the same overall factor equal in absolute value to the number 
Concluding, we just remark the essential points to be taken into account for a choice to be a proper Smilga’s choice: 1) The proper Lagrangian of a quartic massless scalar field should be reproduced multiplicated with an overall factor (negative or positive is not important). 2) The coupling 
Update: Found! After I have extended the search space with my C program, I was able to obtain a set of proper Smilga’s choices for SU(3). These behave exactly as for SU(2). Here is an example
This gives an overall factor 
and things are done! We are left we an interesting mathematical question: As the gauge group is changed the number of proper Smilga’s choices increases vastly. What should be the meaning of such a large number? What kind of symmetry is hidden behind this?
The Gauge Connection 
Okay, I think I’m beginning to understand this, and if I get a little farther, I’ll write a blog post. The A is a choice of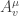
where 
goes t, x, y, z, and v runs over the generators for the group. SU(3) has 8 generators hence the 4×8 form. SU(2) has just 
hence the three components.
Now, if
is a solution to a quartic massless scalar field equation, then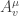 
is a (not completely trivial) solution to the (far more complicated) Yang-Mills classical field equation.
And finally, since the infrared does not need quantum corrections (to first order) this provides a way of getting a problem to begin perturbation theory on.
I think you are on the right track. It was a construction lasted for three years since now but the results surely compensated largely the effort.
Marco
I may be making some progress here. If I do get it, you can be sure that it is so simple that anyone can understand it. This is basically about “all harmonic oscillators are alike” and “all anharmonic oscillators are equivalent”. Another way of saying this is that the non perturbative classical solutions to Yang-Mills have, at their core, a commutative solution. This reminds me of what I’ve been doing with mutually unbiased bases and converting from SU(2) calculations to plain complex numbers.
In your paper 0709.2042, in going from equation (4) to (5), I keep getting the wrong sign
I can’t fix it by assuming I left off a factor of i from the A as happens when sometimes the mathematicians define SU(2).
as in:
This happens no matter which sign convention I choose as it is cancelled out. And since it’s proportional to
By the way, intuitively, another choice for the SU(2) solution would be to make the only thing non zero be the z-component as in:
.
That is, by symmetry you should be able to redirect A, as a vector, in any direction you like and make it pure z.
For some reason, this reminds me of the problem of defining the non Hermitian density matrices in SU(2). They are characterized by two perpendicular vectors, one real, the other imaginary. The squared lengths of the vectors differ by 1. Let’s see if that can be used to create another solution:
.
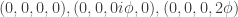Or are these examples going to fail because A will end up as a 4th power and the rotational symmetry of 3-space is broken.
You are right. I have corrected the sign in the proofs of the paper. Also the sign in the Yang-Mills Lagrangian is wrong. Changing this you will get the right result. Sorry for the inconvenience.
Marco
I’ve looked t Smilga’s book on Amazon and I will order it as soon as I am sure I’ve got money for my November rent. It is very clearly written.
It’s clear that any choice of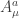
as zero or phi will give a phi^4 Lagrangian. I’m assuming that to choose between them, I have to make the ghost annihilated (which clearly only happens if you assume that the ghost is also equal components so, for example, 
), and that furthermore, I am going to have to prove that the choice is an extremum of the Lagrangian. And to do that last I’m going to have to do a little work.
Carl,
let me say that I appreciate your interest for my work. About the mapping you should consider the following:
1) ‘t Hooft coupling
must be obtained for the coupling.
2) The overall factor must equal the number of degrees of freedom to be carefully preserved. So, I obtain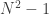
.
The reason for this relies on the fact that I want to reproduce QCD and, in the end, the full QCD Lagrangian will get, for the quarks, a coupling with such a scalar field. When you get rid of it you go back to a Nambu-Jona-Lasinio model. As the right coupling for QCD is ‘t Hooft coupling when you work in the high energy regime and for D=1+1 QCD, this should be maintained.
About the ghost you are right. All the components must be equal to avoid inconsistencies. This will imply immediately that the ghost field decouples.
What is really interesting from a mathematical standpoint is the wide number of proper Smilga’s choice one has. But all I need for my aims is the proof of existence of the mapping. The fact that this map is not unique is not a reason to bother.
Marco
Hi Marco
The physical meaning of Smilga’s choice and its relation to the IR physics of YM eludes me. Suppose SOME solutions (not all) of your field theory (say, YM) are mapped to the solutions of lambda phi^4 scalar QFT. However, other classical solutions (saddle points) of the YM equations of motion also give contribution into the overall partition function of the YM.
How are these classical solutions you are talking about are more important for the IR physics of YM than any other classical solutions?
Cheers
Hi Dmitry,
very nice observation, I should say. The point is the following: I want to do strong perturbation QFT for a Yang-Mills theory. I am fully aware on how it works for a quartic scalar field (see my PRD): I have to do a gradient expansion. When I try this for Y-M I get at the leading order space-homogeneous Y-M equations of motion that are generally impossible to solve as almost all solutions are classically chaotic and so useless to build a QFT. A Smilga’s choice will grant a set of non-chaotic classical solutions to build upon a consistent QFT. Of course there are many solutions following the aforementioned proper Smilga’s choice. So, what I have to consider? It does not matter what is the one you choose but, granted the minimal requirements I said above, the leading order equations you will get to do a gradient expansion, that is a strong coupling expansion, are always the same and you can build a lot of equivalent quantum field theories for Y-M that are nicely manageable. This is all the matter. If you prefer, you can work out this through Heisenberg equations of motion to make the argument clearer.
So, in the end, whatever mapping I takes I will end with the right gluon propagator and spectrum, always the same, for Y-M theory.
Ciao,
Marco
[…] by mapping it on a quartic massless scalar field through the so-called Smilga’s choice (see here). In turn this implies that in all QCD computations we have to manage just a scalar field making […]
Hi Marco
Thanks for the explanation. Let us consider a non-equilibrium formulation of YM (say, Schwinger-Keldysh) and follow the dynamics of the Green functions. Since the EOM for YM admit chaos, this chaos will be inevitably imprinted in the behavior of the Keldysh Green functions, there is no way one can get away with it.
Therefore, for N_c=3 I still have an impression that the sane way to deal with the problem is to learn how to quantize a QFT admitting chaotic behavior in the classical limit: all these chaotic classical solutions contribute into the overall partition function of YM in the eqiulibrium formulation. In non-equilibrium formulation only one saddle point will be important, either with chaos or without, depending on the initial conditions for the Green functions.
Maybe, there is a way to forget about classical trajectories with chaos for N_c \to \infty, and the latter limit might be therefore exactly solvable.
Cheers,
Dmitry.
Hi Dmitry,
I think that when one has to cope with QFT (forget for the moment the non-equilibrium formulation), the main question to be answered is: What are the leading order solutions I should start with? The answer to this question is crucial but, contrarily to what one can think, the right choice is decided in the end by the experiment. When a coupling constant is small we are lucky and we can work with free equations at the leading order. So, the spectrum is seen in nature (electrons, photons,…) that is that of the free theory. Now, You should ask the same question when the coupling is strong: what is the spectrum in this case? We see it in our accelerators everyday: hadrons. From condensed matter analysis this says to me that also in this case solutions must exists, similar to quasi-particles (Landau!!!), that give the spectrum we see. You would not see something like this if you start with classical chaotic solutions. So, this convinces me that nature discards classical chaotic solutions . Of course, if you are able to provide a counterargument to this you are welcome. This by no means implies that the final hadronic spectrum cannot be (quantum) chaotic being just different matters.
So, the question I ask to you is: What are the excitations of a field when the classical solutions are chaotic? You should be able to state it in terms of plane waves to give an answer and I think you are in a serious trouble as no closed form classical chaotic solution is known but, worst, they do not have a Fourier expansion.
But, in my case, things are exactly the contrary. See my recent preprint:
http://arxiv.org/abs/0807.2179
This should give a striking answer to the question.
Ciao,
Marco
Hi Marco
The handron spectrum indeed seems not to carry any information about classical chaotic solutions, so the question is where chaos is hidden in QCD. It might be hidden in the distribution of a flux, which is stochastic and even Gaussian in the large N limit – see for example the book and works by Biro and Matinian Smilga cites in his book, or old idea by Olesen (I think, 1982 paper) about how confinement works in large N limit.
Cheers,
Dmitry.
Hi Dmitry,
Let me point out what is my view about classical chaos and quantum mechanics. I am a true believer into the general insight put forward by Anderson and Laughlin that there is a hierarchy of physical laws and the emergent ones at an higher level may be true complex and unmanageable with respect those at lower levels. So, I think that classical chaos is just an emerging property of the classical laws of physics while, at the quantum level, that is the lower level, there is no chaos at all. As classical physics is an emerging property of a quantum world (let me say in the thermodynamic limit but this is my view), you can see chaos as an emerging property as well. Then, wherever you will look for classical chaos in the quantum laws of physics you will generally meet with disappointment and any attempt is doomed. You will find some works of mine about this matter (check arxiv if you like) and I learned some time ago that a serious definition of quantum chaos does not exist yet. Better, there is one for each physicist working in this field. The reason to be accepted is quite simple: No chaos is expected in a quantum world other than an emerging property.
Ciao,
Marco
[…] think we are currently having a somewhat fruitful discussion with Marco Frasca on his blog. The question is how relevant is chaotic behavior of classical solutions of Yang-Mills […]
Dmitry moved the discussion to his blog. I appreciate his interest and criticisms to my work. The link is here
http://www.nonequilibrium.net/readability/master/75-chaos-ym-confinement/
Of course, whoever else is interested in entering the discussion is surely welcome, here or in the Dmitry’s blog.
Marco
It appears that in Dmitry’s blog comments are moderated so, to avoid further delay, I put my answer here.
————————————————————————————-
Hi Dmitry,
I think you did not answer to the two main questions I put forward to you:
1) Classical chaotic behavior is at odd with experiments
and, at best, you have nothing to compare with.
2) How do you reproduce a well defined spectrum in QFT when a Fourier decomposition in plane waves does not exist?
The recurring question in these latter years about physics is that we have lost the fundamental pragmatic lesson that comes from very far in time: We need numbers to compare with experiments. But a lot of physicists are producing useless theories believing they have reached an understanding. If one has nothing to compare with experiments a theory is nothing. But we are accepting this metaphysical approach today with all the consequences this implies.
Of course, this has nothing to do with you, Dmitry. I do not share your point of view but only experiments (or lattice) can say. Your analysis about non-equilibrium may be as well wrong but I am just asking you to answer my questions for the pure theory. After you have answered these you can extend your analysis to more complex situations. It is a fact that a Smilga’s choice is just a map that brings a Yang-Mills action into a scalar field action. This is true, being a mathematical truth, and independent on any take one may like. Of course, as any kind of mathematics, nature may chooses it or not. Let us wait and see.
Ciao,
Marco
As said above, Dmitry moderates comments, so I anticipate this here.
———————————————————————-
Hi Dmitry,
Of course I cannot see any clear answer to my questions and I can conclude that you are simply evading them. We are doing particle physics and the spectrum are the particles themselves and you cannot get around this claiming that Einstein said blah,blah,blah… It seems to me that you are missing some mundane aspects of quantum field theory (absit iniuria verbis). So, I will keep on discussing with you about this matter again when you will solve Frasca’s conjecture:
A quantum field theory does not exist having as building classical solutions just chaotic solutions.
Please, give me a counterargument and I will be able to appreciate your criticisms. Claiming flaws in other work requires a strong support that you are blatantly missing here. Indeed, your arguments seem deprived of any foundations and as I see no concrete or serious questions against my work I will stop my comments here. People interested can read my latest post
where Dmitry seems to miss another mundane argument about quantum field theory.
Haelfix:
The question of the running coupling in QCD is not mine. With my approach I was able to get back other results. You can look at the work of Boucaud et al.
http://arxiv.org/abs/hep-ph/0212192
published in JHEP. This group obtains a coupling going to zero as the fourth power of momentum. This is in agreement with the scaling of my propagator if you analyze it with a Callan-Symanzik equation. Recently, analysis of experimental data due to Prosperi’s group at University of Milano gets back a similar result. You can see the following paper published on PRL:
http://arxiv.org/abs/0705.0329
So, it seems like the running coupling reaches a trivial fixed point also in the infrared exactly as happens to a massles scalar field theory. Both theories seem to share triviality.
Marco
Dear Marco,
It is a very interesting job!!
I still have some doubts, so, I felt motivated to ask:
Is your approach also valid when temperature is switched on?
How your mapping-theorem deals with spontaneous center-symmetry breaking of gauge group (on pure-YM) at phase transition?
Thank you,
Rafael
Dear Rafael,
Given the gluon propagator the dependence on the temperature is obtained straightforwardly. In my paper http://arxiv.org/abs/0709.2042 you will get the following expression turning back to time and after a Wick rotation turning to Euclidean space
being
the glueball spectrum. As you can see the above expression is identical to the one obtained on the lattice. So, turning to Matsubara frequencies
you get the dependence on the temperature. This result is very useful when you treat the problem of the gluon plasma and I am working on it to obtain hydrodynamic quantities (see my post https://marcofrasca.wordpress.com/2008/10/24/an-inspiring-paper/).
About the second point I do not know the specific problem you are talking about and I appreciate a reference about. But a recent work by Fischer, Maas and Pawloski showed that Dyson-Schwinger equations admit a “massive” solution breaking BRST symmetry (see my post https://marcofrasca.wordpress.com/2008/10/14/a-new-point-of-view/). I should check this point about my mapping but it is anyhow known that the only residual symmetry in the mapping is a conformal symmetry and that mass is dynamically obtained through the self-interaction term.
Marco
Dear Marco,
Thanks a lot!!
The scenario about center-breaking seems to be:
The order parameter for quenched-YM confinement/deconfinement phase-transition is said to be the “Polyakov loop” (PL) (http://books.google.com/books?id=U1hBLG-_WxAC&printsec=frontcover&dq=rothe&hl=pt-PT#PPA493,M1)
At finite-temperature phase transitions the center-group symmetry, which in case of SU(N) is Zn, is dynamically globally broken. It affects observables related to PL (sensitive to Zn-symmetry breaking)
Some universallity arguments use to connect the behaviour of YM at finite T to spin-systems (with Zn global spin-symmetry). On one side “screening masses” can be computed as decay modes of gauge-invariant PL correlation-functions, on the other side, correlation functions of “magnetization-like” observables (in spin-systems) are related to effective masses (i.e. correlation lengths).
Very interesting is that universallity also relates “the screening masses spectrum” of gauge theories (http://xxx.lanl.gov/abs/hep-lat/0302004) which suffer second order phase transitions (such as YM-SU(2) and Ising-model or phi^4) but, not quite exactly for first-order transitions as in SU(3) (http://xxx.lanl.gov/abs/0710.2085), which would be related to q=3 Potts-model.
So, here comes my point, please correct-me:
Smilga´s choice seems to be a general property of YM dynamics, independent of the Lie-group (LG) used as a gauge-group. Thus, it seems to imply that by your approach, at deep infrared, the YM-spectrum is always qualitatively the same (independent of the gauge group or even of a finite-Temp.).
However, when comparing YM-SU(2) and YM-SU(3) at finite-T we see quite different kinds of phase transitions (and distinct screening-masses spectra), so, how would it be possible to explain this phenomena?
Would the same Smilga´s choice be applicable to broken and unbroken phases? How does this tells both phases?
Thanks again!
Best regards,
Rafael
Rafael,
It is not quite true that the spectrum is the exactly the same varying the gauge group. Indeed, for SU(2) and SU(3) the following relation between string tension must hold
This is proved true by lattice computation (see http://prola.aps.org/abstract/PRD/v44/i7/p2090_1) for two colors QCD. Similar relations must hold changing the gauge group and relating it to SU(3) that has
. This implies, in turn, different screening masses.
About the scenario at finite temperature, I have not exploited it so far. What I get is a leading order behavior and so, higher order corrections may enter into the spectrum, corrections that I have neglected so far. Indeed, I have a strong coupling expansion whose higher order corrections I am exploiting just now. More should be said about finite temperature effects. Also in this case, I am just at the very beginning of my studies.
What is the ratio you get for the screening masses between SU(2) and SU(3)? Is it the same of Teper et al.?
Thanks a lot for your interest!
Marco
Dear Rafael,
my approach gives the right ratio between the excited and the ground screening masses as obtained by Fiore et al. in http://arxiv.org/abs/0704.3882.
First of all, I have to thank you for pointing me out the results of this group that are really beautiful. I can sum up their finding in the ratio
being this the ratio between the screening masses for the ground state and the excited state. This result is what I should expect in the confined theory at zero temperature. You should check my paper
http://arxiv.org/abs/0704.3260
and, neglecting the lower state I find (the sigma resonance at about 500 MeV) that is not found on lattice computations but is seen in accelerators, you will see a spectrum going as
starting with n=1 to avoid sigma resonance, and
for m=0 and n=0. You will get exactly 3/2. Please, check also the paper by Craig McNeile http://arxiv.org/abs/0809.2561 with a discussion about such a ratio.
My conclusion is that this ratio is essentially independent on the temperature and the same as for T=0 case.
Marco
I cited the wrong paper by Teper et al. The right one about two colors is
http://prola.aps.org/abstract/PRD/v44/i9/p2869_1
Marco
[…] masses in SU(3) Yang-Mills theory Thanks to a useful comment by Rafael Frigori (see here) I become aware of a series of beautiful papers by an Italian group at Universita’ della […]
[…] we omit the gauge fixing term. Let us fix the gauge group being SU(2). We choose the following (Smilga’s choice, see the […]