Today I have read recent changes to DispersiveWiki. This is a beautiful site about differential equations that is maintained at University of Toronto by Jim Colliander and has notable contributors as the Fields medallist Terence Tao. Terry introduced a new page about Liouville’s equation as he got involved with it in a way you can read here. Physicists working on quantum gravity has been aware of this equation since eighties as it is the equation of two-dimensional quantum gravity and comes out quite naturally in string theory. A beautiful paper about quantum field theory of Liouville equation is due to Roman Jackiw and one of his collaborators Eric D’Hoker (see here). But what people could have overlooked is that Liouville’s equation is the equation of the Ricci soliton in two dimensions. The reason is that in this case a set of isothermal coordinates can always be found and the metric is always conformal, that is
being 
being 
and finally for the Ricci soliton one has
being 
Turning back to the Jackiw and D’Hoker paper, we can see that a 2D gravity theory emerges naturally as the equilibrium (Ricci soliton) solution of a Fokker-Planck (Ricci flow) equation. This scenario seems a beautiful starting point to build an understanding of quantum gravity. I am still thinking about a lot and I will put all this on a paper one day.
The Gauge Connection 
Speaking of gravity, check this out :
http://arxiv.org/abs/0901.4005
Implications of Graviton-Graviton Interaction to Dark Matter
Authors: A. Deur
(Submitted on 26 Jan 2009)
Abstract: Our present understanding of the universe requires the existence of dark matter and dark energy. We discuss here a natural mechanism that could make exotic dark matter and possibly dark energy unnecessary: just as the non-abelian nature of the strong force increases the binding of quarks, the gravitational binding of matter may be similarly increased for large massive systems such as galaxies, making exotic dark matter superfluous. A lattice calculation quantitatively supports the relevance of this process for spiral galaxies, dwarf spiral galaxies and galaxy clusters. This mechanism explains naturally the cosmic coincidence problem.
Dear Daniel,
Thanks for the hint. I have checked this paper and I would like to start from a higher level view to reach similar conclusions.
Marco
Hi marco,
The best part here it is that this was done in a lattice. Do you agree with the aproximation?
Dear Daniel,
I have worked also in general relativity taking the non-linearities as the leading term of a perturbation series (see http://arxiv.org/abs/hep-th/0508246) in agreement with the duality principle in perturbation theory granting a perturbation series in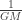
for GR. This permits to understand what is going on near singularities where the gravitational field is indeed strong.
It appears that, when you try to quantize such a leading order solution, assuming all equal components to map on a scalar field, you fall back on a continuous spectrum, i.e. no mass gap and so no confinement. This is in agreement e.g. with 2D gravity and quantized Liouville equation. So, I expect that if GR is the right theory to describe gravitational binding, it cannot be enough to explain dark matter in the light this is done in the paper you cite unless you modify properly Einstein equations.
So, I can agree that a similar effect as for QCD, applied to GR, can produce the right corrections to account for dark matter but the price is that you modify GR equations.
Marco
Hi Marco,
But would it be possible that same strong expantion is more or less valid for a weak gravitational field but large distances, but not at medium ranges? That is, it would be like rescaling the system, given that as you go far away from a singularity, M would rescale to zero very fast away from the nucleus, given that the galactical density exponentialy decreses. This expantion ceases to agree with the newtonian expantion anyway.
Which means that, in the leading order, the description galaxy, far away of the center, not at in infinity,much outiside the galaxy, though, which is dual to that of one near a singularity. For exemple, a galaxy would have, away from the nucleus, a description similar to one near the ring singularity of a kerr black hole, at leading order. It should also agree with any resuld of your paper given that galaxies are more or less 2D.
Dear Daniel,
While the scenario you propose could be more or less plausible, you are anyway in a hurry to show that the model postulated in the paper is indeed obtainable from GR equations in a way that gives ground to the description you gave.
Marco
Hi Marco,
Yes, you are right. That’s why I am asking you 🙂 You are specialist in lattice QCD.
Dear Daniel,
I am a theoretical physicist working in QCD, the theory in the continuous not on lattice. Anyhow, in this paper there is a severe demanding for a support to the phenomenological model that was proposed. From my preceding comments you can obtain my view about and I think that a modification to GR equations is required. Of course, if the author of the paper is able to give arguments against this conclusion, I will be very happy to change my view.
Marco
Hi Frasca,
I’m sorry. I judged you by a specialist on lattice given the number of posts on this subject! I feel embarrassed now!
Dear Daniel,
You shouldn’t. I work a lot with people doing computations on lattice and I have a great appreciation of their work. Anyhow, I have also appreciated your comments. Keep on doing that.
Marco
[…] a quite interesting result that I have discussed in the comments of a preceding post of mine (see here): 2d general relativity has no confinement as a quantum field theory. 2d general relativity can […]