Where we are now?

Summer conferences passed by, we have more precise data on the Higgs particle and some new results were announced. So far, this particle appears more and more in agreement with the Standard Model expectations without no surprise in view. Several measurements were performed with the full dataset at 140 . Most commentators avoid to tell about this because it does not warrant click-bait anymore. At EPS-HEP 2019 in Ghent (Belgium), the following slide was presented by Hulin Wang on behalf of the ATLAS Collaboration

There appears to be an excess at 250 GeV and another at 700 GeV but we are talking of about 2 sigma, nothing relevant. Besides, ATLAS keeps on seeing an excess in the vector boson fusion for ZZ decay, again about 2 sigma, but CMS sees nothing, rather they are somewhat on the missing side!

No evidence of supersymmetry whatsoever, neither the multiplet of Higgs nor charged Higgs are seen that could hint to supersymmetry. I would like to remember that some researchers were able to obtain the minimal supersymmetric standard model from string theory and so, this is a diriment aspect of the experimental search. Is the Higgs particle just the first one of an extended sector of electroweak (soft) supersymmetry breaking?

So, why could the slide I just posted be so important? The interesting fact is the factor 2 between the mass of this presumed new resonance and that of the Higgs particle. The Higgs sector of the Standard Model can be removed from it and treated independently. Then, one can solve it exactly and the spectrum is given by an integer multiple of the mass of the Higgs particle. This is exactly the spectrum of a Kaluza-Klein particle and it would represents an indirect proof of the existence of another dimension in space. So, if confirmed, we would move from a desolating scenario with no new (beyond standard model) physics in view to a completely overturned situation! We could send all the critics back to sleep wishing them a better luck for the next tentative.

Back to reality, the slide yields the result for the dataset of 36.1 and no confirmation from CMS has ever arrived. We can just hope that the dreaming scenario takes life.

Cracks in the Witten’s index theorem?

In these days, a rather interesting paper (see here for the preprint) appeared on Physical Review Letters. These authors study a Wess-Zumino model for , the prototype of any further SUSY model, and show that there exists an anomaly at one loop in perturbation theory that breaks supersymmetry. This is rather shocking as the model is supersymmetric at the classical level and, in agreement with Witten’s index theorem, no breaking of supersymmetry should ever be observed. Indeed, the authors, in the conclusions, correctly ask how the Witten’s theorem copes with this rather strange behavior. Of course, Witten’s theorem is correct and the question comes out naturally and is very much interesting for further studies.

This result is important as I have incurred in a similar situation for the Wess-Zumino model in a couple of papers. The first one (see here and here)  went published and shows how the classical Wess-Zumino model, in a strong coupling regime, breaks supersymmetry. Therefore, I asked a similar question as for the aforementioned case: How quantum corrections recover the Witten’s theorem? The second one is remained a preprint (see here). I tried to send it to Physics Letters B but the referee, without any check of mathematics, just claimed that there was the Witten’s theorem to forbid my conclusions. The Editor asked me to withdraw the paper in view of this identical reason. This was a very strong one. So, I never submited this paper again and just checked the classical case where I was more lucky.

So, my question is still alive: Has supersymmetry in itself the seeds of its breaking?

This is really important in view of the fact that the Minimal Supersymmetric Standard Model (MSSM), now in disgrace after LHC results, can have a dark side in its soft supersymmetry breaking sector. This, in turn, could entail a wrong understanding of where the superpartners could be after the breaking. Anyway, it is really something exciting already at the theoretical level. We are just stressing Witten’s index theorem in search for answers.

ICHEP 2018

The great high-energy physics conference ICHEP 2018 is over and, as usual, I spend some words about it. The big collaborations of CERN presented their last results. I think the most relevant of this is about the evidence () that the Standard Model is at odds with the measurement of spin correlation between top-antitop pair of quarks. More is given in the ATLAS communicate. As expected, increasing precision proves to be rewarding.

About the Higgs particle, after the important announcement about the existence of the ttH process, both ATLAS and CMS are pursuing further their improvement of precision. About the signal strength they give the following results. For ATLAS (see here)

and CMS (see here)

The news is that the error is diminished and both agrees. They show a small tension, 13% and 17% respectively, but the overall result is consistent with the Standard Model.

When the different contributions are unpacked in the respective contributions due to different processes, CMS claims some tensions in the WW decay that should be taken under scrutiny in the future (see here). They presented the results from data and so, there is no significant improvement, for the moment, with respect to Moriond conference this year. The situation is rather better for the ZZ decay where no tension appears and the agreement with the Standard Model is there in all its glory (see here). Things are quite different, but not too much, for ATLAS as in this case they observe some tensions but these are all below (see here). For the WW decay, ATLAS does not see anything above (see here).

So, although there is something to take under attention with the increase of data, that will reach this year, but the Standard Model is in good health with respect to the Higgs sector even if there is a lot to be answered yet and precision measurements are the main tool. The correlation in the tt pair is absolutely promising and we should hope this will be confirmed a discovery.

 

Something to say but not yet…

Last week I have been in Montpellier to attend QCD 17 Conference hosted at the CNRS and whose mainly organizer is Stephan Narison. At this conference participates a lot of people from CERN presenting new results very nearly to the main summer conferences. This year, QCD 17 was in conjuction with EPSHEP 2017 were the new results coming from LHC were firstly presented. This means that the contents of the talks in the two conferences just superposed in a matter of few hours.

On Friday, the last day of conference, I posted the following twitter after attending the talk by Shunsuke Honda on behalf of ATLAS at QCD 17:

and the reason was this slide

The title of the talk was “Cross sections and couplings of the Higgs Boson from ATLAS”. As you can read from it, there is a deviation of about 2 sigmas from the Standard Model for the Higgs decaying to ZZ(4l) for VBF. Indeed, they can claim agreement yet but it is interesting anyway (maybe are we missing anything?). The previous day at EPSHEP 2017, Ruchi Gupta on behalf of ATLAS presented an identical talk with the title “Measurement of the Higgs boson couplings and properties in the diphoton, ZZ and WW decay channels using the ATLAS detector” and the slide was the following:

The result is still there but with a somewhat sober presentation. What does this mean? Presently, this amounts to very few. We are still within the Standard Model even if something seems to peep out. In order to claim a discovery, this effect should be seen with a lower error and at CMS too. The implications would be that there could be a more complex spectrum of the Higgs sector with a possible new understanding of naturalness if such a spectrum would not have a formal upper bound. People at CERN promised more data coming in the next weeks. Let us see what will happen to this small effect.

Well below 1%

When a theory is too hard to solve people try to consider lower dimensional cases. This also happened for Yang-Mills theory. The four dimensional case is notoriously difficult to manage due to the large coupling and the three dimensional case has been treated both theoretically and by lattice computations. In this latter case, the ground state energy of the theory is known very precisely (see here). So, a sound theoretical approach from first principles should be able to get that number at the same level of precision. We know that this is the situation for Standard Model with respect to some experimental results but a pure Yang-Mills theory has not been seen in nature and we have to content ourselves with computer data. The reason is that a Yang-Mills theory is realized in nature just in interaction with other kind of fields being these scalars, fermions or vector-like.

In these days, I have received the news that my paper on three dimensional Yang-Mills theory has been accepted for publication in the European Physical Journal C. Here is tha table for the ground state for SU(N) at different values of N compared to lattice data

N Lattice     Theoretical Error

2 4.7367(55) 4.744262871 0.16%

3 4.3683(73) 4.357883714 0.2%

4 4.242(9)     4.243397712 0.03%

∞ 4.116(6)    4.108652166 0.18%

These results are strikingly good and the agreement is well below 1%. This in turn implies that the underlying theoretical derivation is sound. Besides, the approach proves to be successful both also in four dimensions (see here). My hope is that this means the beginning of the era of high precision theoretical computations in strong interactions.

Andreas Athenodorou, & Michael Teper (2017). SU(N) gauge theories in 2+1 dimensions: glueball spectra and k-string tensions J. High Energ. Phys. (2017) 2017: 15 arXiv: 1609.03873v1

Marco Frasca (2016). Confinement in a three-dimensional Yang-Mills theory arXiv arXiv: 1611.08182v2

Marco Frasca (2015). Quantum Yang-Mills field theory Eur. Phys. J. Plus (2017) 132: 38 arXiv: 1509.05292v2

Yang-Mills theory paper gets published!

Exact solutions of quantum field theories are very rare and, normally, refer to toy models and pathological cases. Quite recently, I put on arxiv a pair of papers presenting exact solutions both of the Higgs sector of the Standard Model and the Yang-Mills theory made just of gluons. The former appeared a few month ago (see here) while the latter has been accepted for publication a few days ago (see here). I have updated the latter just today and the accepted version will appear on arxiv on 2 January next year.

What does it mean to solve exactly a quantum field theory? A quantum field theory is exactly solved when we know all its correlation functions. From them, thanks to LSZ reduction formula, we are able to compute whatever observable in principle being these cross sections or decay times. The shortest way to correlation functions are the Dyson-Schwinger equations. These equations form a set with the former equation depending on the higher order correlators and so, they are generally very difficult to solve. They were largely used in studies of Yang-Mills theory provided some truncation scheme is given or by numerical studies. Their exact solutions are generally not known and expected too difficult to find.

The problem can be faced when some solutions to the classical equations of motion of a theory are known. In this way there is a possibility to treat the Dyson-Schwinger set. Anyhow, before to enter into their treatment, it should be emphasized that in literature the Dyson-Schwinger equations where managed just in one way: Using their integral form and expressing all the correlation functions by momenta. It was an original view by Carl Bender that opened up the way (see here). The idea is to write the Dyson-Schwinger equations into their differential form in the coordinate space. So, when you have exact solutions of the classical theory, a possibility opens up to treat also the quantum case!

This shows unequivocally that a Yang-Mills theory can display a mass gap and an infinite spectrum of excitations. Of course, if nature would have chosen the particular ground state depicted by such classical solutions we would have made bingo. This is a possibility but the proof is strongly related to what is going on for the Higgs sector of the Standard Model that I solved exactly but without other matter interacting. If the decay rates of the Higgs particle should agree with our computations we will be on the right track also for Yang-Mills theory. Nature tends to repeat working mechanisms.

Marco Frasca (2015). A theorem on the Higgs sector of the Standard Model Eur. Phys. J. Plus (2016) 131: 199 arXiv: 1504.02299v3

Marco Frasca (2015). Quantum Yang-Mills field theory arXiv arXiv: 1509.05292v1

Carl M. Bender, Kimball A. Milton, & Van M. Savage (1999). Solution of Schwinger-Dyson Equations for ${\cal PT}$-Symmetric Quantum Field Theory Phys.Rev.D62:085001,2000 arXiv: hep-th/9907045v1

In the aftermath of ICHEP 2016

ATLAS and CMS nuked our illusions on that bump. More than 500 papers were written on it and some of them went through Physical Review Letters. Now, we are contemplating the ruins of that house of cards. This says a lot about the situation in hep in these days. It should be emphasized that people at CERN warned that that data were not enough to draw a conclusion and if they fix the threshold at a reason must exist. But carelessness acts are common today if you are a theorist and no input from experiment is coming for long.

It should be said that the fact that LHC could confirm the Standard Model and nothing else is one of the possibilities. We should hope that a larger accelerator could be built, after LHC decommissioning, as there is a long way to the Planck energy that we do not know how to probe yet.

What does it remain? I think there is a lot yet. My analysis of the Higgs sector is still there to be checked as I will explain in a moment but this is just another way to treat the equations of the Standard Model, not beyond it. Besides, for the end of the year they will reach , almost triplicating the actual integrated luminosity and something interesting could ever pop out. There are a lot of years of results ahead and there is no need to despair. Just to wait. This is one of the most important activities of a theorist. Impatience does not work in physics and mostly for hep.

About the signal strength, things seem yet too far to be settled. I hope to see better figures for the end of the year. ATLAS is off the mark, going well beyond unity for WW, as happened before. CMS claimed for WW decay, worsening their excellent measurement of reached in Run I. CMS agrees fairly well with my computations but I should warn that the error bar is yet too large and now is even worse. I remember that the signal strength is obtained by the ratio of the measured cross section to the one obtained from the Standard Model. The fact that is smaller does not necessarily mean that we are beyond the Standard Model but that we are just solving the Higgs sector in a different way than standard perturbation theory. This solution entails higher excitations of the Higgs field but they are strongly depressed and very difficult to observe now. The only mark could be the signal strength for the observed Higgs particle. Finally, the ZZ channel is significantly less sensible and error bars are so large that one can accommodate whatever she likes yet. Overproduction seen by ATLAS is just a fluctuation that will go away in the future.

The final sentence to this post is what we have largely heard in these days: Standard Model rules.

Higgs or not Higgs, that is the question

LHCP2016 is running yet with further analysis on 2015 data by people at CERN. We all have seen the history unfolding since the epochal event on 4 July 2012 where the announcement of the great discovery happened. Since then, also Kibble passed away. What is still there is our need of a deep understanding of the Higgs sector of the Standard Model. Quite recently, LHC restarted operations at the top achievable and data are gathered and analysed in view of the summer conferences.

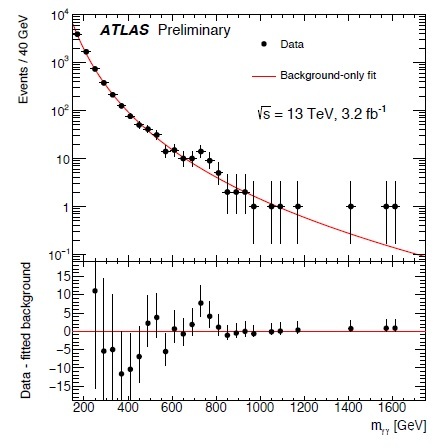
The scalar particle observed at CERN has a mass of about 125 GeV. Data gathered on 2015 seem to indicate a further state at 750 GeV but this is yet to be confirmed. Anyway, both ATLAS and CMS see this bump in the data and this seems to follow the story of the discovery of the Higgs particle. But we have not a fully understanding of the Higgs sector  yet. The reason is that, in run I, gathered data were not enough to reduce the error bars to such small values to decide if Standard Model wins or not. Besides, as shown by run II, further excitations seem to pop up. So, several theoretical proposals for the Higgs sector still stand up and could be also confirmed already in August this year.

Indeed, there are great news already in the data presented at LHCP2016. As I pointed out here, there is a curious behavior of the strengths of the signals of Higgs decay in and some tension, even if small, appeared between ATLAS and CMS results. Indeed, ATLAS seemed to have seen more events than CMS moving these contributions well beyond the unit value but, as CMS had them somewhat below, the average was the expected unity agreeing with expectations from the Standard Model. The strength of the signals is essential to understand if the propagator of the Higgs field is the usual free particle one or has some factor reducing it significantly with contributions from higher states summing up to unity. In this case, the observed state at 125 GeV would be just the ground state of a tower of particles being its excited states. As I showed recently, this is not physics beyond the Standard Model, rather is obtained by solving exactly the quantum equations of motion of the Higgs sector (see here). This is done considering the other fields interacting with the Higgs field just a perturbation.

So, let us do a recap of what was the situation for the strength of the signals for the decays of the Higgs particle. At LHCP2015 the data were given in the following slide

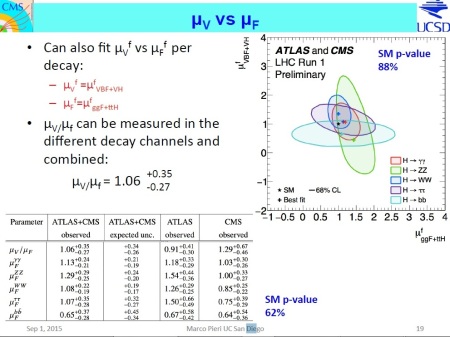
From the table one can see that the signal strengths for decays in ATLAS are somewhat beyond unity while in CMS these are practically unity for but, more interestingly, 0.85 for . But we know that data gathered for decay are largely more than for decay. The error bars are large enough to be not a concern here. The value 0.85 is really in agreement with the already cited exact computations from the Higgs sector but, within the error, in overall agreement with the Standard Model. This seems to point toward on overestimated number of events in ATLAS but a somewhat reduced number of events in CMS, at least for 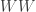decay.

At LHCP2016 new data have been presented from the two collaborations, at least for the decay. The results are striking. In order to see if the scenario provided from the exact solution of the Higgs sector is in agreement with data, these should be confirmed from run II and those from ATLAS should go down significantly. This is indeed what is going on! This is the corresponding slide

This result is striking per se as shows a tendency toward a decreasing value when, in precedence, it was around unity. Now it is aligned with the value seen at CMS for the 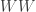decay! The value seen is again in agreement with that given in the exact solution of the Higgs sector. And ATLAS? This is the most shocking result: They see a significant reduced set of events and the signal strength they obtain is now aligned to the one of CMS (see Strandberg’s talk at page 11).

What should one conclude from this? If the state at 750 GeV should be confirmed, as the spectrum given by the exact solution of the Higgs sector is given by an integer multiplied by a mass, this would be at 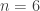. Together with the production strengths, if further data will confirm them, the proper scenario for the breaking of electroweak symmetry is exactly the one described by the exact solution. Of course, this should be obviously true but an experimental confirmation is essential for a lot of reasons, last but not least the form of the Higgs potential that, if the numbers are these, the one postulated in the sixties would be the correct one. An other important reason is that coupling with other matter does not change the spectrum of the theory in a significant way.

So, to answer to the question of the title remains to wait a few weeks. Then, summer conferences will start and, paraphrasing Coleman: God knows, I know and by the end of the summer we all know.

Marco Frasca (2015). A theorem on the Higgs sector of the Standard Model Eur. Phys. J. Plus (2016) 131: 199 arXiv: 1504.02299v3

Quantum gravity

Quantum gravity appears today as the Holy Grail of physics. This is so far detached from any possible experimental result but with a lot of attentions from truly remarkable people anyway. In some sense, if a physicist would like to know in her lifetime if her speculations are worth a Nobel prize, better to work elsewhere. Anyhow, we are curious people and we would like to know how does the machinery of space-time work this because to have an engineering of space-time would make do to our civilization a significant leap beyond.

A fine recount of the current theoretical proposals has been rapidly presented by Ethan Siegel in his blog. It is interesting to notice that the two most prominent proposals, string theory and loop quantum gravity, share the same difficulty: They are not able to recover the low-energy limit. For string theory this is a severe drawback as here people ask for a fully unified theory of all the interactions. Loop quantum gravity is more limited in scope and so, one can think to fix the problem in a near future. But of all the proposals Siegel is considering, he is missing the most promising one: Non-commutative geometry. This mathematical idea is due to Alain Connes and earned him a Fields medal. So far, this is the only mathematical framework from which one can rederive the full Standard Model with all its particle content properly coupled to the Einstein’s general relativity. This formulation works with a classical gravitational field and so, one can possibly ask where quantized gravity could come out. Indeed, quite recently, Connes, Chamseddine and Mukhanov (see here and here), were able to show that, in the context of non-commutative geometry, a Riemannian manifold results quantized in unitary volumes of two kind of spheres. The reason why there are two kind of unitary volumes is due to the need to have a charge conjugation operator and this implies that these volumes yield the units in the spectrum. This provides the foundations for a future quantum gravity that is fully consistent from the start: The reason is that non-commutative geometry generates renormalizable theories!

The reason for my interest in non-commutative geometry arises exactly from this. Two years ago, I, Alfonso Farina and Matteo Sedehi obtained a publication about the possibility that a complex stochastic process is at the foundations of quantum mechanics (see here and here). We described such a process like the square root of a Brownian motion and so, a Bernoulli process appeared producing the factor 1 or i depending on the sign of the steps of the Brownian motion. This seemed to generate some deep understanding about space-time. Indeed, the work by Connes, Chamseddine and Mukhanov has that understanding and what appeared like a square root process of a Brownian motion today is just the motion of a particle on a non-commutative manifold. Here one has simply a combination of a Clifford algebra, that of Dirac’s matrices, a Wiener process and the Bernoulli process representing the scattering between these randomly distributed quantized volumes. Quantum mechanics is so fundamental that its derivation from a geometrical structure with added some mathematics from stochastic processes makes a case for non-commutative geometry as a serious proposal for quantum gravity.

I hope to give an account of this deep connection in a near future. This appears a rather exciting new avenue to pursue.

Ali H. Chamseddine, Alain Connes, & Viatcheslav Mukhanov (2014). Quanta of Geometry: Noncommutative Aspects Phys. Rev. Lett. 114 (2015) 9, 091302 arXiv: 1409.2471v4

Ali H. Chamseddine, Alain Connes, & Viatcheslav Mukhanov (2014). Geometry and the Quantum: Basics JHEP 12 (2014) 098 arXiv: 1411.0977v1

Farina, A., Frasca, M., & Sedehi, M. (2013). Solving Schrödinger equation via Tartaglia/Pascal triangle: a possible link between stochastic processing and quantum mechanics Signal, Image and Video Processing, 8 (1), 27-37 DOI: 10.1007/s11760-013-0473-y

News from CERN

Two days ago, CERN presented their new results at 13 TeV to the World. Of course, collected data so far are not enough for conclusive results but the these are exciting anyway. The reason is that both the collaborations, CMS and ATLAS, see a bump at around 750 GeV in the decay. Summing up the results of the two collaborations, they are around without look elsewhere effect, not yet a discovery but, probably, at the summer conferences they will have something more conclusive to say. This could be an unlucky fluctuation but this situation remember us the story of the discovery of the Higgs boson more than three years ago. The question if this is beyond Standard Model physics is what I will try to answer in these few lines.

Firstly, if this particle is real, it decays with two photons exactly as the Higgs boson. Secondly, with a final state like this it can have only spin 0 or 2. We will be conservative and assume that this is not a graviton. Rather, it is a sibling of the Higgs particle. Besides, it was not observed in run I but is not inconsistent with data from there. It appears like the increased luminosity favored its appearance. We want to be more conservative and we take for granted just the Lagrangian of the Standard Model. So, what is this beast?

My answer is that this could be an excited state of the Higgs boson that, having a production rate lower than its ground state seen at run I, needed more luminosity to be observed. You do not need to change the Lagrangian of the Standard Model for this and it is not BSM physics yet. You do not even need a technicolor theory to describe it. The reason is that the Higgs part of the Standard Model can be treated mathematically yielding exact solutions. The quantum field theory can be exactly solved and the spectrum of the theory says exactly what I stated above (see here, and here). The Higgs model per se is exactly solvable. So, Jester’s idea to add another scalar field to the Lagrangian model is useless, it is all just inside and you will get a two photon final state as well.

Of course, it is too early to draw a final conclusion and a wealth of papers with a prompt explanation flooded arxiv in these two days. With the restart of LHC on spring and the collecting of more data, things will be clearer than now. For the moment, this hint is enough to keep us excited for the next few months.

Marco Frasca (2015). A theorem on the Higgs sector of the Standard Model arxiv arXiv: 1504.02299v2

Marco Frasca (2015). Quantum Yang-Mills field theory arxiv arXiv: 1509.05292v1