Where does mass come from?

After CERN’s updates (well recounted here, here and here) producing no real news but just some concern about possible Higgs cloning, I would like to discuss here some mathematical facts about what one should expect about mass generation and why we should not be happy with these results, now coming out on a quarterly basis.

The scenario we are facing so far is one with a boson particle resembling more and more the Higgs particle appearing in the original formulation of the Standard Model. No trace is seen of anything else at higher energies, no evidence of supersymmetry. It appears like no new physics is hiding here rather for it we will have to wait eventually the upgrade of LHC that will start its runs on 2015.

I cannot agree with all of this and this is not the truth at all. The reason to not believe all this is strictly based on theoretical arguments and properties of partial differential equations. We are aware that physicists can be skeptical also about mathematics even if this is unacceptable as mathematics has no other way than being true or false. There is nothing like a half truth but there are a lot of theoretical physicists trusting on it. I have always thought that being skeptical on mathematics is just an excuse to avoid to enter into other work. There could always be the risk that one discovers it is correct and then has to support it.

The point is the scalar field. A strong limitation we have to face when working in quantum field theory is that only small coupling can be managed. No conclusive analysis can be drawn when a coupling is just finite and also lattice computations produce confusion. It seems like small coupling only can exist and all the theory we build are in the hope that nature is benign and yields nothing else than that. For the Higgs field is the same. All our analysis are based on this, the hierarchy problem comes out from this. Just take any of your textbook on which you built your knowledge of this matter and you will promptly realize that nothing else is there. Peschin and Schroeder, in their really excellent book, conclude that strong coupling cannot exist in quantum field theory and the foundation of this argument arises from renormalization group. Nature has only small couplings.

Mathematics, a product of nature, has not just small couplings and nobody can impede a mathematician to take these equations and try to analyze them with a coupling running to infinity. Of course, I did it and somebody else tried to understand this situation and the results make the situation rather embarrassing.

These reflections sprang from a paper appeared yesterday on arxiv (see here). In a de Sitter space there is a natural constant having the dimension of energy and this is the Hubble constant (in natural units). It is an emerging result that a massless scalar field with a quartic interaction in such a space develops a mass. This mass goes like $m^2\propto \sqrt{\lambda}H^2$ being $\lambda$ the coupling coming from the self-interaction and $H$ the Hubble constant. But the authors of this paper are forced to turn to the usual small coupling expansion just singling out the zero mode producing the mass. So, great news but back to the normal.

A self-interacting scalar field has the property to get mass by itself. Generally, such a self-interacting field has a potential in the form $\frac{1}{2}\mu^2\phi^2+\frac{\lambda}{4}\phi^4$ and we can have three cases $\mu^2>0$ , $\mu^2=0$ and $\mu^2<0$ . In all of them the classical equations of motion have an exact massive free solution (see here and Tao’s Dispersive Wiki) when $\lambda$ is finite. These solutions cannot be recovered by any small coupling expansion unless one is able to resum the infinite terms in the series. The cases with $\mu^2\ne 0$ are interesting in that this term gets a correction depending on $\lambda$ and for the case $\mu^2<0$ one can recover a spectrum with a Goldstone excitation and the exact solution is an oscillating one around a finite value different from zero (it never crosses the zero) as it should be for spontaneous breaking of symmetry. But the mass is going like $\sqrt{\lambda}\Lambda^2$ where now $\Lambda$ is just an integration constant. The same happens in the massless case as one recovers a mass going like $m^2\propto\sqrt{\lambda}\Lambda^2$ . We see the deep analogy with the scalar field in a de Sitter space and these authors are correct in their conclusions.

The point here is that the Higgs mechanism, as has been devised in the sixties, entails all the philosophy of "small coupling and nothing else" and so it incurs in all the possible difficulties, not last the hierarchy problem. A modern view about this matter implies that, also admitting $\mu^2<0$ makes sense, we have to expand around a solution for $\lambda$ finite being this physically meaningful rather than try an expansion for a free field. We are not granted that the latter makes sense at all but is just an educated guess.

What does all this imply for LHC results? Indeed, if we limit all the analysis to the coupling of the Higgs field with the other fields in the Standard Model, this is not the best way to say we have observed a true Higgs particle as the one postulated in the sixties. It is just curious that no other excitation is seen beyond the (eventually cloned) 126 GeV boson seen so far but we have a big desert to very high energies. Because the very nature of the scalar field is to have massive solutions as soon as the self-interaction is taken to be finite, this also means that other excited states must be seen. This simply cannot be the Higgs particle, mathematics is saying no.

M. Beneke, & P. Moch (2012). On “dynamical mass” generation in Euclidean de Sitter space arXiv arXiv: 1212.3058v1

Marco Frasca (2009). Exact solutions of classical scalar field equations J.Nonlin.Math.Phys.18:291-297,2011 arXiv: 0907.4053v2

This entry was posted on Sunday, December 16th, 2012 at 1:14 pm and is filed under Mathematical Physics, Particle Physics, Physics. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

9 Responses to Where does mass come from?

amarashiki says:

16/12/2012 at 2:28 pm

I have written some basic post on notions of mass in my thread of special relativity http://thespectrumofriemannium.wordpress.com/2012/06/19/log020-emc%C2%B2-the-notion-of-mass/

Reply
Adam says:

16/12/2012 at 9:01 pm

Hi,
I’m having a look at your J.Nonlin.Math.Phys paper, and there is something I don’t understand. If I’m right, you are studying a scalar field with one component (it’s a real field, and in the O(N) terminology, it is the case N=1). In euclidian space, this field theory is related to the Ising model. In particular, because the symmetry \phi \to -\phi is discrete, there is no Goldstone mode.
I don’t really understand why you say after equation 3.12 that you have a zero mode, as \epsilon_0 is different from zero…

We nevertheless expect a phase transition for this model at some finite (and negative) \mu_0^2, so you should definitely have a zero mode for some value of your parameters. Is that the case ?

Have you tried to solve the case of a complex field. Here you should expect a Goldstone mode.

Cheers,

Adam

Reply
- mfrasca says:
  
  16/12/2012 at 9:43 pm
  
  Dear Adam,
  
  Thank you for your interest about my paper. Eq.(3.12) is in the quantum treatment of these solutions and applies just at the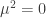 $\mu^2=0$ case. That is the reason why I have a zero mode here.
  
  For $\mu^2<0$ I have worked out this analysis elsewhere (see http://arxiv.org/abs/hep-th/0703203) and I have got the spectrum with a Goldstone mode.
  
  For the complex field these solutions have the form of a complex phase factor multiplying such massive solutions. All that is seen there also applies in this case.
  
  Marco
  
  Reply
  - Adam says:
    
    17/12/2012 at 5:21 pm
    
    Hi,
    I don’t really get it…
    -Because of the quantum fluctuations, you would expect that for \mu_0^2<0 but close enough to zero, the symmetry stays unbroken (it is broken at the mean-field level, but quantum fluctuations destroy it).
    -Because it is a real field, you should not find a Goldstone mode, right ? And in any case the formula for $\epsilon_n shows that it is never 0, even fon n=0.
    -For the complexe field, do you mean that the phase is not dynamical ? That's for sure not the case.
    
    Cheers,
    
    Adam
    
    Reply
    - mfrasca says:
      
      17/12/2012 at 5:38 pm
      
      Hi Adam,
      
      I hope we agree that these classical solutions do satisfy the given equations of motion for any value of $\mu^2$ . But you can use your preferred symbolic mathematical tool and check this.
      
      1) Sure.
      
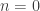      2) The point is that, for $\mu^2<0$ (is this the case you are considering here?), the exact classical solution is given by a $\rm dn$ Jacobi function. In this case, if you perform a quantum analysis, assuming this is your zero mode to be singled out, the spectrum has the form $\epsilon_n=n\epsilon_0$ being $n=0,1,2,\ldots$ . I just called the $n=0$ excitation the Goldstone mode.
      
      3) For the complex case, the classical exact solutions take the form $\phi=e^{i\alpha}\phi_0$ , being $\phi_0$ the solution of the equation for the single component. You can try by yourself by substitution into the equations of motion but it is just a trivial application of the idea that all the components are taken to be equal.
      
      I have not proved the uniqueness of these classical solutions but the interesting point is that they satisfy a massive dispersion relation. The corresponding quantum field theory displays also the interesting feature to be trivial at the leading order.
      
      Marco
ohwilleke says:

19/12/2012 at 2:54 am

FYI, I explore some of the issues that your analysis in this post raises at: http://dispatchesfromturtleisland.blogspot.com/2012/12/does-sm-require-excited-higgs-bosons.html

Feel free to correct any misinterpretations or inaccuracies that you identify.

Reply
Vladimir Kalitvianski says:

07/01/2013 at 6:57 pm

Dear Marco,

So, what is the true mechanism for particle masses? Self-action? Or, maybe, it is better to use phenomenological masses?

Reply
- mfrasca says:
  
  07/01/2013 at 7:41 pm
  
  Dear Vladimir,
  
  So far, there are some mechanisms found that produce masses for massless fields. Most known ones are Higgs mechanism and Nambu-Jona-Lasino dynamical breaking of symmetry. In both cases the field acquires a non-null value on vacuum. This appears somewhat different from a mechanism devised by Schwinger that, instead, shows how self-interaction of the field (or if you like non-linearities) is the main actor producing mass. This can already be seen at a classical level as such self-interacting fields, when the self-interaction coupling is finite and not taken to go to zero, display massive solutions. It is interesting to see that even when the fields are massive, such classical solutions produce finite corrections to the mass. This is true also when you consider a Higgs-like Lagrangian and you have not even to check if there is a non-null vacuum expectation value. Rather this appears true a posteriori. It is interesting to note that when a scalar field like this interacts with a Fermion field, a Nambu-Jona-Lasinio model is immediately obtained. So, all the mechanisms cited so far are entangled in some way.
  
  In the end, only experiment will say to us what is the proper one. Now, it is just a matter of personal taste and nothing else. Higgs mechanism is the most widely accepted even if no sound experimental verification exists at the moment. It is up to people at CERN to say if this is also the mechanism of choice for nature and presently they are those having more information about on Earth on this.
  
  Classical solutions point to a situation where this Higgs-like particle found at LHC cannot be alone. This is what I discuss in my post. You can check such solutions by yourself using my paper and a tool for symbolic mathematics on computer. No much effort is needed.
  
  I am eager to know from CERN if some interesting news is coming out in the next few months. But I will not tear my hairs off if things will not go this way.
  
  Cheers,
  
  Marco
  
  Reply
Vladimir Kalitvianski says:

07/01/2013 at 7:50 pm

Thank you, Marco, for your answer. I personally do not like self-action (non-linear) mechanism. I am for a phenomenological way of writing mass terms.

Reply