Notwithstanding LHC has seen the particle, the Higgs sector of the Standard Model has some serious problems. This fact yielded more than one headache to physicists. One of these difficulties is called technically “triviality“.  The scalar field theory, that is so well defined classically, does not exist as a quantum field theory unless is non-interacting. There is a wonderful paper by Michael Aizenman that shows that this is true for dimensions 5 and higher. So, one should think that, as we live in four dimensions, there is no reason to worry. The point is that Michael Aizenman left the question in four dimensions open. So, does Higgs particle exist or not and how does it yield mass if it will not interact? CERN said to us that Higgs particle is there and so, in some way, the scalar sector of the Standard Model must properly work. Aizenman’s proof was on 1981 but what is the situation now? An answer is in this article on Scholarpedia. As stated by the author Ulli Wolff
The scalar field theory, that is so well defined classically, does not exist as a quantum field theory unless is non-interacting. There is a wonderful paper by Michael Aizenman that shows that this is true for dimensions 5 and higher. So, one should think that, as we live in four dimensions, there is no reason to worry. The point is that Michael Aizenman left the question in four dimensions open. So, does Higgs particle exist or not and how does it yield mass if it will not interact? CERN said to us that Higgs particle is there and so, in some way, the scalar sector of the Standard Model must properly work. Aizenman’s proof was on 1981 but what is the situation now? An answer is in this article on Scholarpedia. As stated by the author Ulli Wolff
Triviality of lattice phi^4 theory in this sense has been rigorously proven for D>4 while for the most interesting borderline case D=4 we have only partial results but very strong evidence from numerical simulations.
While there is another great expert on quantum field theory, Franco Strocchi, in his really worth to read book saying
The recent proof of triviality of phi^4 in 3 + 1 spacetime dimensions indicates that the situation becomes worse in the real world, and in particular the renormalized perturbative series of the phi^4 model seems to have little to do with the non-perturbative solution.
We see that experts do not completely agree about the fact that a proof exists or not but, for sure, the scalar theory in four dimensions cannot interact and the Standard Model appears in serious troubles.
Before to enter more in details about this matter, let me say that, even if Strocchi makes no citation about where the proof is, he is the one being right. We have proof about this, the matter is now well understood and again we are waiting for the scientific community to wake up. Also, the Standard Model is surely secured and there is no serious risk about the recent discovery by CERN of the Higgs particle.
The proof has been completed recently by Renata Jora with this paper on arxiv. Renata extended the proof an all the energy range. I met her in Montpellier (France) at this workshop organized by Stephan Narison. We have converging interests in research. Renata’s work is based on a preceding proof, due to me and Igor Suslov, showing that, at large coupling, the four dimensional theory is indeed trivial. You can find the main results here and here. Combining these works together, we can conclude that Strocchi’s statement is correct but there is no harm for the Standard Model as we will discuss in a moment. Also the fact that the perturbation solution of the model is not properly describing the situation can be seen from the strictly non-analytical behaviours seen at strong coupling that makes impossible to extend what one gets at small coupling to that regime.
The fact that CERN has indeed seen the Higgs particle and that the Higgs sector of the Standard Model is behaving properly, unless a better understanding will emerge after the restart of the LHC, has been seen with the studies of the propagators of the Yang-Mills theory in the Landau gauge. The key paper is this where the behaviour of the running coupling of the theory was obtained on all the energy range from lattice computations.
This behaviour shows that, while the theory is trivial at both the extremes of the energy range, there is an intermediate regime where we can trust the theory and treat it as an effective one. There the coupling does not run to zero but moves around some finite non-null value. Of course, all this is just saying that this theory must be superseded by an extended one going to higher energies (supersymmetry? Technicolor?) but it is reasonable to manage the theory as if all this just works at current energies. Indeed, LHC has shown that a Higgs particle is there.
So, triviality is saying that the LHC will find something new for sure. Today, beams moved again inside the accelerator. We are eager to see what will come out form this wonderful enterprise.
Aizenman, M. (1981). Proof of the Triviality of Field Theory and Some Mean-Field Features of Ising Models for Physical Review Letters, 47 (12), 886-886 DOI: 10.1103/PhysRevLett.47.886
Renata Jora (2015). $Φ^4$ theory is trivial arXiv arXiv: 1503.07298v1
Marco Frasca (2006). Proof of triviality of $λφ^4$ theory Int.J.Mod.Phys.A22:2433-2439,2007 arXiv: hep-th/0611276v5
Igor M. Suslov (2010). Asymptotic Behavior of the \Beta Function in the Φ^4 Theory: A Scheme
Without Complex Parameters J.Exp.Theor.Phys.111:450-465,2010 arXiv: 1010.4317v1
I. L. Bogolubsky, E. -M. Ilgenfritz, M. Müller-Preussker, & A. Sternbeck (2009). Lattice gluodynamics computation of Landau-gauge Green’s functions in the deep infrared Phys.Lett.B676:69-73,2009 arXiv: 0901.0736v3



[…] The gauge connection: That Higgs is trivial! […]
Hi Marco,
I’ve seen the arxiv paper of Jora, and I couldn’t make any sense of it. For example, I don’t think equation 11 of her paper is meaningful (since the partition function is independent of momenta, you cannot do a derivation of it to get the 2-point correlation functions). Furthermore, I don’t see where dimension play a role here. And we know for sure that in d<4, the theory is not trivial…
Could you shed light on these points ?
Best
Adam
Dear Adam,
Thank you for the comment. I agree about eq.(11). This does not make sense unless one takes and then a derivative with respect to momenta. But then this is no more a functional derivative with respect to
and then a derivative with respect to momenta. But then this is no more a functional derivative with respect to 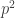 . This does not seem to harm too much. In any case, it would be helpful to hear from the author.
. This does not seem to harm too much. In any case, it would be helpful to hear from the author.
Best
Marco
This might not be a problem other than notation. However, I am more concerned about my other remark on dimensionality…
Best
Adam
About dimensionality just consider that this proof relies on a preceding Jora’s work http://arxiv.org/abs/1403.2227 and you should check also this for a full understanding.
I briefly skimmed through Jora’s paper and read in page 1 that no attempt at renormalization is made. I gather that we are not talking about Wick ordered $\phi^4$, but rather a theory with quartic interaction and no counter-terms, somehow… Am I understanding this correctly?
Please, as said above, check the published work of Jora on PLB on which the proof relies on.
it would help to resolve these problems by lifting up your heads from and looking to nature for solutions. The foundations of physics must be revisited to make any progress.
Done. Please, feel free to read all the material here. If you will have difficulties to see where revolutions are, do not hesitate to get in touch with me for help.